Incomplete Cholesky Factorization
From CFD-Wiki
(Difference between revisions)
| Line 8: | Line 8: | ||
In other words we have <br> | In other words we have <br> | ||
'''L <math>\bullet</math>L<sup>T</sup> = A ''' <br> | '''L <math>\bullet</math>L<sup>T</sup> = A ''' <br> | ||
| + | |||
| + | === Algorithm for full matrix ''A'' === | ||
| + | We have by definition | ||
| + | <math> | ||
| + | L_{ij}^T = L_{ji} | ||
| + | </math> <br> | ||
| + | From this we can easily obtain<br> | ||
| + | <math> | ||
| + | L_{ii} = \left( {a_{ii} - \sum\limits_{k = 1}^{i - 1} {L_{ik}^2 } } \right)^{{1 \over 2}} | ||
| + | </math><br> | ||
| + | and <br> | ||
| + | <math> | ||
| + | L_{ji} = {1 \over {L_{ii} }}\left( {a_{ij} - \sum\limits_{k = 1}^{i - 1} {L_{ik} L_{jk} } } \right) | ||
| + | </math> ; where j = i+1, i+2, ..., N <br> | ||
| + | Given this, we can easily construct the factor '''L''' by solving from i := 1, 2, ..., N | ||
Revision as of 06:37, 14 September 2005
Cholesky Factorization
When the square matrix A is symmetric and positive definite then it has an efficient triangular decomposition. Symmetric means that aij = aji for i,j = 1, ... , N. While positive definite means that

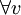
In cholesky factorization we construct a lower triangular matrix L whose transpose LT can itself serve as upper triangular part.
In other words we have
L  LT = A
LT = A
Algorithm for full matrix A
We have by definition
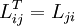
From this we can easily obtain
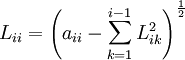
and
 ; where j = i+1, i+2, ..., N
; where j = i+1, i+2, ..., N
Given this, we can easily construct the factor L by solving from i := 1, 2, ..., N
