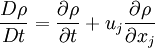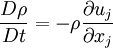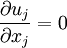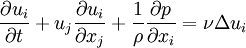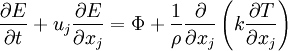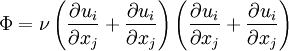Incompressible flow
From CFD-Wiki
(Added a sentece about approximation for low Ma number) |
|||
| Line 1: | Line 1: | ||
A flow is said to be incompressible if the density of a fluid element does not change during its motion. It is a property of the flow and not of the fluid. The rate of change of density of a material fluid element is given by the material derivative | A flow is said to be incompressible if the density of a fluid element does not change during its motion. It is a property of the flow and not of the fluid. The rate of change of density of a material fluid element is given by the material derivative | ||
| - | <math> | + | :<math> |
\frac{D \rho}{D t} = \frac{\partial \rho}{\partial t} + u_j \frac{\partial \rho}{\partial x_j} | \frac{D \rho}{D t} = \frac{\partial \rho}{\partial t} + u_j \frac{\partial \rho}{\partial x_j} | ||
</math> | </math> | ||
| Line 7: | Line 7: | ||
From the continuity equation we have | From the continuity equation we have | ||
| - | <math> | + | :<math> |
\frac{D \rho}{D t} = - \rho \frac{\partial u_j}{\partial x_j} | \frac{D \rho}{D t} = - \rho \frac{\partial u_j}{\partial x_j} | ||
</math> | </math> | ||
Hence the flow is incompressible if the divergence of the velocity field is identically zero. Note that the density field need not be uniform in an incompressible flow. All that is required is that the density of a fluid element should not change in time as it moves through space. For example, flow in the ocean can be considered to be incompressible even though the density of water is not uniform due to stratification. | Hence the flow is incompressible if the divergence of the velocity field is identically zero. Note that the density field need not be uniform in an incompressible flow. All that is required is that the density of a fluid element should not change in time as it moves through space. For example, flow in the ocean can be considered to be incompressible even though the density of water is not uniform due to stratification. | ||
| + | |||
| + | [[Compressible flow]] can with good accuracy be approximated as incompressible if the [[Mach number]] is below 0.3. | ||
== Governing Equations == | == Governing Equations == | ||
| + | |||
The [[Navier Stokes Equations | Navier Stokes equations]] for incompressible flow are | The [[Navier Stokes Equations | Navier Stokes equations]] for incompressible flow are | ||
* Continuity equation | * Continuity equation | ||
| - | <math> | + | :<math> |
\frac{\partial u_j}{\partial x_j} = 0 | \frac{\partial u_j}{\partial x_j} = 0 | ||
</math> | </math> | ||
| Line 24: | Line 27: | ||
* Momentum equation | * Momentum equation | ||
| - | <math> | + | :<math> |
\frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j} + \frac{1}{\rho} \frac{\partial p}{\partial x_i} = \nu \Delta u_i | \frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j} + \frac{1}{\rho} \frac{\partial p}{\partial x_i} = \nu \Delta u_i | ||
</math> | </math> | ||
| Line 30: | Line 33: | ||
* Energy equation | * Energy equation | ||
| - | <math> | + | :<math> |
\frac{\partial E}{\partial t} + u_j \frac{\partial E}{\partial x_j} = \Phi + \frac{1}{\rho} \frac{\partial}{\partial x_j} \left( k \frac{\partial T}{\partial x_j} \right) | \frac{\partial E}{\partial t} + u_j \frac{\partial E}{\partial x_j} = \Phi + \frac{1}{\rho} \frac{\partial}{\partial x_j} \left( k \frac{\partial T}{\partial x_j} \right) | ||
</math> | </math> | ||
| Line 41: | Line 44: | ||
* <math>\Phi</math> is the rate of dissipation of mechanical energy per unit mass | * <math>\Phi</math> is the rate of dissipation of mechanical energy per unit mass | ||
| - | <math> | + | :<math> |
\Phi = \nu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_i}{\partial x_j} \right) | \Phi = \nu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_i}{\partial x_j} \right) | ||
\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_i}{\partial x_j} \right) | \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_i}{\partial x_j} \right) | ||
| Line 51: | Line 54: | ||
== Physical characteristics == | == Physical characteristics == | ||
| - | A consequence of incompressible flow is that there is no equation of state for pressure unlike in compressible flow. Since there is no separate equation for pressure it must be obtained from the continuity and momentum equations. The main role of pressure is to satisfy the zero divergence condition of the velocity field. Note that pressure is only determined upto a constant. | + | |
| + | A consequence of incompressible flow is that there is no equation of state for pressure unlike in [[compressible flow]]. Since there is no separate equation for pressure it must be obtained from the continuity and momentum equations. The main role of pressure is to satisfy the zero divergence condition of the velocity field. Note that pressure is only determined upto a constant. | ||
If the viscosity is assumed to be constant then the energy equation is decoupled from the continuity and momentum equations. | If the viscosity is assumed to be constant then the energy equation is decoupled from the continuity and momentum equations. | ||
Revision as of 12:27, 13 September 2005
A flow is said to be incompressible if the density of a fluid element does not change during its motion. It is a property of the flow and not of the fluid. The rate of change of density of a material fluid element is given by the material derivative
From the continuity equation we have
Hence the flow is incompressible if the divergence of the velocity field is identically zero. Note that the density field need not be uniform in an incompressible flow. All that is required is that the density of a fluid element should not change in time as it moves through space. For example, flow in the ocean can be considered to be incompressible even though the density of water is not uniform due to stratification.
Compressible flow can with good accuracy be approximated as incompressible if the Mach number is below 0.3.
Governing Equations
The Navier Stokes equations for incompressible flow are
- Continuity equation
- Momentum equation
- Energy equation
where
-
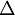 is the Laplacian operator
is the Laplacian operator
- E is the internal energy per unit mass
-
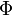 is the rate of dissipation of mechanical energy per unit mass
is the rate of dissipation of mechanical energy per unit mass
-
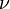 is the kinematic viscosity
is the kinematic viscosity
- k is the coefficient of thermal conductivity
- T is the temperature
Physical characteristics
A consequence of incompressible flow is that there is no equation of state for pressure unlike in compressible flow. Since there is no separate equation for pressure it must be obtained from the continuity and momentum equations. The main role of pressure is to satisfy the zero divergence condition of the velocity field. Note that pressure is only determined upto a constant.
If the viscosity is assumed to be constant then the energy equation is decoupled from the continuity and momentum equations.