Introduction to turbulence/Reynolds averaged equations
From CFD-Wiki
(→The origins of turbulence) |
(→The origins of turbulence) |
||
| Line 215: | Line 215: | ||
So we hypothesized a base flow which was laminar and showed that it is unchanged even with the imposition of infintesimal disturbances on it - ''but only as long as the disturbances'' '''remain''' ''infinitesimal!'' What happens if the disturbance starts to grow? Obviously before we conclude that all laminar flows are laminar forever we better investigate whether or not these infinitesimal disturbances can grow to ''finite'' size. To do this we need an equation for the fluctuation itself. | So we hypothesized a base flow which was laminar and showed that it is unchanged even with the imposition of infintesimal disturbances on it - ''but only as long as the disturbances'' '''remain''' ''infinitesimal!'' What happens if the disturbance starts to grow? Obviously before we conclude that all laminar flows are laminar forever we better investigate whether or not these infinitesimal disturbances can grow to ''finite'' size. To do this we need an equation for the fluctuation itself. | ||
| - | An equation for the | + | An equation for the fluctuation (which might be an imposed disturbance) can be obtained by subtracting the equation for the mean (or base) flow from that for the instantaneous motion. We already did this for the continuity equation. Now we will do it for the momentum equation. Subtracting equation 3.13 from equation 3.11 yields an equation for the fluctuation as: |
Revision as of 04:23, 25 June 2006
Contents |
The Reynolds averaged equations and the turbulence closure problem
The equations governing the instantaneous fluid motions
All fluid motions, whether turbulent or not, are governed by the dynamical equations for a fluid. These can be written using Cartesian tensor notation as:
|
| (2.1) |
|
| (2.2) |
where 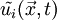 represents the i-the component of the fluid velocity at a point in space,
represents the i-the component of the fluid velocity at a point in space,![[\vec{x}]_i=x_i](/W/images/math/3/3/7/337ed91923252ad11afe7b37c91c8372.png) , and time,t. Also
, and time,t. Also
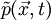 represents the static pressure,
represents the static pressure, 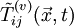 , the viscous(or deviatoric) stresses, and
, the viscous(or deviatoric) stresses, and 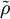 the fluid density. The tilde over the symbol indicates that an instantaneous quantity is being considered. Also the Einstein summation convention has been employed.
the fluid density. The tilde over the symbol indicates that an instantaneous quantity is being considered. Also the Einstein summation convention has been employed.
In equation 2.1, the subscript 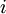 is a free index which can take on the values 1,2 and 3. Thus equation 2.1 is in reality three separate equations. These three equations are just Newton's second law written for a continuum in a spatial(or Eulerian) reference frame. Together they relate the rate of change of momentum per unit mass
is a free index which can take on the values 1,2 and 3. Thus equation 2.1 is in reality three separate equations. These three equations are just Newton's second law written for a continuum in a spatial(or Eulerian) reference frame. Together they relate the rate of change of momentum per unit mass 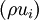 ,a vector quantity, to the contact and body forces.
,a vector quantity, to the contact and body forces.
Equation 2.2 is the equation for mass conservation in the absence of sources(or sinks) of mass. Almost all flows considered in this material will be incompressible, which implies that derivative of the density following the fluid material[the term in brackets] is zero. Thus for incompressible flows, the mass conservation equation reduces to:
|
| (2.3) |
From equation 2.2 it follows that for incompressible flows,
|
| (2.4) |
The viscous stresses(the stress minus the mean normal stress) are represented by the tensor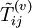 . From its definition,
. From its definition,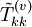 =0. In many flows of interest, the fluid behaves as a Newtonian fluid in which the viscous stress can be related to the fluid motion by a constitutive relation of the form.
=0. In many flows of interest, the fluid behaves as a Newtonian fluid in which the viscous stress can be related to the fluid motion by a constitutive relation of the form.
|
| (2.5) |
The viscosity, 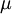 , is a property of the fluid that can be measured in an independent experiment.
, is a property of the fluid that can be measured in an independent experiment. 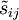 is the instantaneous strain rate tensor defined by
is the instantaneous strain rate tensor defined by
|
| (2.6) |
From its definition, 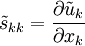 . If the flow is incompressible,
. If the flow is incompressible, 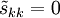 and the Newtonian constitutive equation reduces to
and the Newtonian constitutive equation reduces to
|
| (2.7) |
Throughout this material, unless explicitly stated otherwise, the density 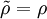 and the viscosity
and the viscosity 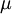 will be assumed constant. With these assumptions, the instantaneous momentum equations for a Newtonian Fluid reduce to:
will be assumed constant. With these assumptions, the instantaneous momentum equations for a Newtonian Fluid reduce to:
|
| (2.8) |
where the kinematic viscosity, 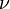 , has been defined as:
, has been defined as:
|
| (2.9) |
Note that since the density is assumed constant, the tilde is no longer necessary.
Sometimes it will be more instructive and convenient to not explicitly include incompressibilty in the stress term, but to refer to the incompressible momentum equation in the following form:
|
| (2.10) |
This form has the advantage that it is easier to keep track of the exact role of the viscous stresses.
Equations for the average velocity
Although laminar solutions to the equations often exist that are consistent with the boundary conditions, perturbations to these solutions(sometimes even infinitesimal) can cause them to become turbulent. To see how this can happen, it is convenient to analyze the flow in two parts, a mean(or average) component and a fluctuating component. Thus the instantaneous velocity and stresses can be written as:
|
| (2.11) |
Where 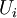 ,
, 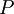 and
and 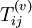 represent the mean motion, and
represent the mean motion, and 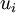 ,
, 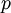 and
and 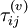 the fluctuating motions. This technique for decomposing the instantaneous motion is referred to as the Reynolds decomposition. Note that if the averages are defined as ensemble means, they are, in general, time-dependent. For the remainder of this material unless other wise stated, the density will be assumed constant so
the fluctuating motions. This technique for decomposing the instantaneous motion is referred to as the Reynolds decomposition. Note that if the averages are defined as ensemble means, they are, in general, time-dependent. For the remainder of this material unless other wise stated, the density will be assumed constant so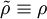 ,and its fluctuation is zero.
,and its fluctuation is zero.
Substitution of equations 2.11 into equations 2.10 yields
|
| (2.12) |
This equation can now be averaged to yield an equation expressing momentum conservation for the averaged motion. Note that the operations of averaging and differentiation commute; i.e., the average of a derivative is the same as the derivative of the average. Also the average of a fluctuating quantity is zero. Thus the equation for the averaged motion reduces to:
|
| (2.13) |
where the remaining fluctuating product term has been moved to the right hand side of the equation. Whether or not the last term is zero like the other fluctuating term depends on the correlation of the terms in the product. In general, these correlations are not zero.
The mass conservation equation can be similarly decomposed. In incompressible form, substitution of equations 2.11 into equation 2.4 yields:
|
| (2.14) |
of which average is
|
| (2.15) |
It is clear from the equation 2.15 that the averaged motion satisfies the same form of the mass conservation equation as does the instantaneous motion at least for incompressible flows. How much simpler the turbulence problem would be if the same were true for the momentum! Unfortunately, as is easily seen from the equation 2.13, such is not the case.
Equation 2.15 can be subtracted from equation 2.14 to yield an equation for instantaneous motion alone; i.e,
|
| (2.16) |
Again, like the mean, the form of the original instantaneous equation is seen to be preserved. The reason, of course, is obvious: the continuity equation is linear. The momentum equation , on the other hand, is not; hence the difference.
Equation 2.16 can be used to rewrite the last term in equation 2.13 for the mean momentum. Multiplying equation 2.16 by 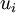 and averaging yields:
and averaging yields:
|
| (2.17) |
This can be added to: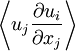 to obtain:
to obtain:
|
| (2.18) |
Where again the fact that arithmetic and averaging operations commute has been used.
The equation for the averaged momentum, equation 2.13 can now be rewritten as:
|
| (2.19) |
The last two terms on the right hand side are both divergence terms and can be combined; the result is:
|
| (2.20) |
Now the terms in square brackets on the right have the dimensions of stress. The first term is, in fact , the viscous stress. The second term, on the other hand, is not a stress at all, but simply a re-worked version of the fluctuating contribution to the non-linear acceleration terms. The fact that it can be written this way, however, indicates that at least as far as the motion is concerned, it acts as though it were a stress- hence its name, the Reynolds stress. In the succeeding sections the consequences of this difference will be examined.
The turbulence problem
It is the appearance of the Reynolds stress which makes the turbulence problem so difficult - at least from the engineers perspective. Even though we can pretend it is a stress, the physics which give rise to it are very different from the viscous stress. The viscous stress can be related directly to the other flow properties by constitutive equations, which in turn depend only on the properties of the fluid( as in equation 2.5 for a Newtonian fluid). The reason this works is that when we make such closure approximations for a fluid, we are averaging over characteristic length and time scales much smaller than those of the flows we are interested in. Yet at the same time, these scales are much larger than the molecular length and time scales which characterize the molecular interactions that are actually causing the momentum transfer. (This is what the continuum approximation is all about).
The Reynolds stress, on the other hand, arises from the flow itself! Worse, the scales of the fluctuating motion which give rise to it are the scales we are interested in. This means that the closure ideas which worked so well for the viscous stress, should not be expected to work too well for the Reynolds stress. And as we shall see, they do not.
This leaves us in a terrible position. Physics and engineering are all about writing equations(and boundary conditions) so we can solve them to make predictions. We don't want to have a build prototype airplanes first to see if they will they fall out of the sky. Instead we want to be able to analyze our designs before building, to save the cost in money and lives if our ideas are wrong. The same is true for dams and bridges and tunnels and automobiles. If we had confidence in our turbulence models, we could even build huge one-offs and expect them to work the first time. Unfortunately, even though turbulence models have improved to the point where we can use them in design, we still cannot trust them enough to eliminate expensive wind tunnel and model studies. And recent history is full of examples to prove this.
The turbulence problem (from the engineers perspective) is then three-fold:
- The averaged equations are not closed. Count the number of unknowns in equation 2.20 above. Then count the number of equations. Even with the continuity equation we have atleast six equations too few.
- The simple ideas to provide the extra equations usually do not work. And even when we can fix them up for a particular class of flows (like the flow in a pipe, for example), they will most likely not be able to predict what happens in even a slightly different environment(like a bend).
- Even the last resort of compiling engineering tables for design handbooks carries substantial risk. This is the last resort for the engineer who lacks equations or cannot trust them. Even when based on a wealth of experience, they require expensive model testing to see if they can be extrapolated to a particular situation. Often they cannot, so infinitely clever is Mother Nature in creating turbulence that is unique to a particular set of boundary conditions.
Turbulent flows are indeed flows!. And that is the problem.
The origins of turbulence
Turbulent flows can often be observed to arise from laminar flows as the Reynolds number, (or someother relevant parameter) is increased. This happens because small disturbances to the flow are no longer damped by the flow, but begin to grow by taking energy from the original laminar flow. This natural process is easily visualized by watching the simple stream of water from a faucet (or even a pitcher). Turn the flow on very slow (or pour) so the stream is very smooth initially, at least near the outlet. Now slowly open the faucet (or pour faster) abd observe what happens, first far away, then closer to the spout. The surface begins to exhibit waves or ripples which appear to grow downstream . In fact, they are growing by extracting energy from the primary flow. Eventually they grow enough that the flow breaks into drops. These are capillary instabilities arisiing from surface tension, but regardless of the type of instability, the idea is the same -small (or infinitesimal ) disturbances have grown to disrupt the serenity (and simplicity) of laminar flow.
The manner in which the instabilities grow naturally in a flow can be examined using the equations we have already developed above. We derived them by decomposing the motion into a mean and fluctuating part. But suppose instead we had decomposed the motion into a base flow part (the initial laminar part) and into a disturbance which represents a fluctuating part superimposed on the base flow. The result of substituting such a decomposition into the full Navier-Stokes equations and averaging is precisely that given by equations 2.13 and 2.15. But the very important difference is the additional restriction that what was previously identified as the mean (or averaged ) motion is now also the base or laminar flow.
Now if the base flow is really laminar flow (which it must be by our original hypothesis), then our averaged equations governing the base flow must yield the same mean flow as the original laminar flow on which the disturbances was superimposed. But this can happen only if these new averaged equations reduce to exactly the same lamiane flow equations without any evidence of a disturbance. Clearly from equations 2.13 and 2.15, this can happen only if all the Reynolds stress terms vanish identically! Obviously this requires that the disturbances be infintesimal so the extra terms can be neglected - hence our interest in infinitesimal disturbances.
So we hypothesized a base flow which was laminar and showed that it is unchanged even with the imposition of infintesimal disturbances on it - but only as long as the disturbances remain infinitesimal! What happens if the disturbance starts to grow? Obviously before we conclude that all laminar flows are laminar forever we better investigate whether or not these infinitesimal disturbances can grow to finite size. To do this we need an equation for the fluctuation itself.
An equation for the fluctuation (which might be an imposed disturbance) can be obtained by subtracting the equation for the mean (or base) flow from that for the instantaneous motion. We already did this for the continuity equation. Now we will do it for the momentum equation. Subtracting equation 3.13 from equation 3.11 yields an equation for the fluctuation as:

![\rho\left[\frac{\partial \tilde{u}_i}{\partial t}+\tilde{u}_j\frac{\partial \tilde{u}_i}{\partial x_j}\right] = -\frac{\partial \tilde{p}}{\partial x_i}+\frac{\partial \tilde{T}_{ij}^{(v)}}{\partial x_j}](/W/images/math/6/a/5/6a5eb7f60bcc4f1a6489784007a98d0a.png)
![\left[\frac{\partial \tilde{\rho}}{\partial t}+\tilde{u}_j\frac{\partial \tilde{\rho}}{\partial x_j}\right]+ \tilde{\rho}\frac{\partial \tilde{u}_j}{\partial x_j}= 0](/W/images/math/1/7/4/1746e47f4400c67af0751b99076a68a5.png)
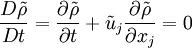
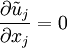
![\tilde{T}_{ij}^{(v)}= 2\mu[\tilde{s}_{ij}-\frac{1}{3}\tilde{s}_{kk}\delta_{ij}]](/W/images/math/5/c/5/5c5e17af620383642e9581d23417c5f4.png)
![\tilde{s}_{ij}= \frac{1}{2}\left[\frac{\partial \tilde u_i}{\partial x_j}+\frac{\partial \tilde u_j}{\partial x_i}\right]](/W/images/math/e/2/8/e286f63b1f3d528a051c14b02bb7f7fb.png)
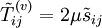
![\left[\frac{\partial \tilde{u}_i}{\partial t}+\tilde{u}_j\frac{\partial \tilde{u}_i}{\partial x_j}\right] = -\frac {1}{\tilde\rho}\frac{\partial \tilde{p}}{\partial x_i}+\nu\frac{\partial^2 {\tilde{u}_i}}{\partial x_j^2}](/W/images/math/4/a/a/4aa21b3de5a327d14c9c3cacf6ab712b.png)
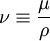
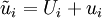
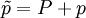
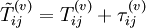
![\rho\left[\frac{\partial (U_i+u_i)}{\partial t}+(U_j+u_j)\frac{\partial (U_i+u_i)}{\partial x_j}\right] = -\frac{\partial (P+p)}{\partial x_i}+\frac{\partial (T_{ij}^{(v)}+\tau_{ij}^{(v)})}{\partial x_j}](/W/images/math/e/c/e/ece4821f7ebe7cfa3730586cef936eaf.png)
![\rho\left[\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}\right] = -\frac{\partial P}{\partial x_i}+\frac{\partial T_{ij}^{(v)}}{\partial x_j}-\rho\left \langle u_j\frac{\partial u_i }{\partial x_j} \right \rangle](/W/images/math/9/e/8/9e822214474bc0033d98d8c2e4f5a577.png)
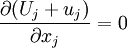
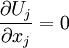
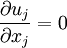
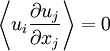
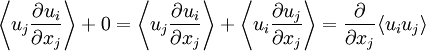
![\rho\left[\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}\right] = -\frac{\partial P}{\partial x_i}+\frac{\partial T_{ij}^{(v)}}{\partial x_j}-\frac{ \partial}{\partial x_j}{(\rho\left \langle u_iu_j\right \rangle)}](/W/images/math/b/7/f/b7f65cb20813481a7c2f2f8c3503f436.png)
![\rho\left[\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}\right] = -\frac{\partial P}{\partial x_i}+\frac{\partial }{\partial x_j}[T_{ij}^{(v)}-{\rho\left \langle u_iu_j\right \rangle}]](/W/images/math/2/a/1/2a1fb4efafd51bafbb0223502b886cd1.png)