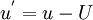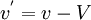Introduction to turbulence/Statistical analysis/Multivariate random variables
From CFD-Wiki
(→Joint pdfs and joint moments) |
(→Joint pdfs and joint moments) |
||
| Line 18: | Line 18: | ||
</math> | </math> | ||
</td><td width="5%">(2)</td></tr></table> | </td><td width="5%">(2)</td></tr></table> | ||
| + | |||
| + | where as before capital letters are usd to represent the mean values. Clearly the fluctuating quantities <math>u^{'}</math> and <math>v^{'}</math> are random variables with zero man. | ||
| + | |||
| + | A psitive value of <math>\left\langle u^{'}v^{'} \right\rangle </math> indicates that <math>u^{'}</math> and <math>v^{'}</math> tend to vary together. A negative value indicates | ||
=== The bi-variate normal (or Gaussian) distribution === | === The bi-variate normal (or Gaussian) distribution === | ||
dssd | dssd | ||
Revision as of 08:15, 2 June 2006
Joint pdfs and joint moments
Often it is importamt to consider more than one random variable at a time. For example, in turbulence the three components of the velocity vector are interralated and must be considered together. In addition to the marginal (or single variable) statistical moments already considered, it is necessary to consider the joint statistical moments.
For example if 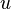 and
and 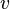 are two random variables, there are three second-order moments which can be defined
are two random variables, there are three second-order moments which can be defined 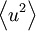 ,
, 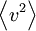 , and
, and 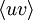 . The product moment
. The product moment 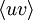 is called the cross-correlation or cross-covariance. The moments
is called the cross-correlation or cross-covariance. The moments 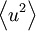 and
and 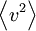 are referred to as the covariances, or just simply the variances. Sometimes
are referred to as the covariances, or just simply the variances. Sometimes 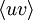 is also referred to as the correlation.
is also referred to as the correlation.
In a manner similar to that used to build-up the probabilility density function from its measurable counterpart, the histogram, a joint probability density function (or jpdf),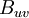 , can be built-up from the joint histogram. Figure 2.5 illustrates several examples of jpdf's which have different cross correlations. For convenience the fluctuating variables
, can be built-up from the joint histogram. Figure 2.5 illustrates several examples of jpdf's which have different cross correlations. For convenience the fluctuating variables 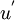 and
and 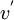 can be defined as
can be defined as
|
| (2) |
|
| (2) |
where as before capital letters are usd to represent the mean values. Clearly the fluctuating quantities 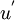 and
and 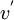 are random variables with zero man.
are random variables with zero man.
A psitive value of 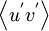 indicates that
indicates that 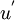 and
and 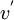 tend to vary together. A negative value indicates
tend to vary together. A negative value indicates
The bi-variate normal (or Gaussian) distribution
dssd