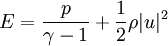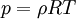Inviscid flow
From CFD-Wiki
(fixed spelling) |
|||
| (8 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | A flow in which viscous effects can be neglected is known as ''inviscid flow''. At high Reynolds numbers, flow past slender bodies involve thin boundary layers. Viscous effects are important only inside the boundary layer and the flow outside it is nearly inviscid. If the boundary layer is not separated then the inviscid flow model can be used to predict the pressure distribution with reasonable accuracy. | + | A flow in which viscous effects can be neglected is known as ''inviscid flow''. At high Reynolds numbers, flow past slender bodies involve thin boundary layers. Viscous effects are important only inside the boundary layer and the flow outside it is nearly inviscid. If the boundary layer is not separated then the inviscid flow model can be used to predict the pressure distribution with reasonable accuracy. Although no practical flow is inviscid, the inviscid assumption is valid if the time scales for diffusion are much larger compared to the time scales for convection, which is measured by the [[Reynolds number]]. |
==Governing Equations== | ==Governing Equations== | ||
| - | The governing equations for inviscid flow, also known as ''Euler equations'', are obtained by discarding the viscous terms from the Navier-Stokes equations | + | The governing equations for inviscid flow, also known as ''Euler equations'', are obtained by discarding the viscous terms from the [[Navier-Stokes equations]] |
*Continuity equation | *Continuity equation | ||
| - | <math> | + | :<math> |
\frac{\partial \rho}{\partial t} + \frac{\partial}{\partial x_j}(\rho u_j)= 0 | \frac{\partial \rho}{\partial t} + \frac{\partial}{\partial x_j}(\rho u_j)= 0 | ||
</math> | </math> | ||
| Line 12: | Line 12: | ||
*Momentum equation | *Momentum equation | ||
| - | <math> | + | :<math> |
\frac{\partial}{\partial t}(\rho u_i) + \frac{\partial}{\partial x_j}(\rho u_i u_j + p \delta_{ij}) = 0 | \frac{\partial}{\partial t}(\rho u_i) + \frac{\partial}{\partial x_j}(\rho u_i u_j + p \delta_{ij}) = 0 | ||
</math> | </math> | ||
| Line 18: | Line 18: | ||
*Energy equation | *Energy equation | ||
| - | <math> | + | :<math> |
\frac{\partial}{\partial t}(\rho E) + \frac{\partial}{\partial x_j}[(\rho E + p)u_j] = 0 | \frac{\partial}{\partial t}(\rho E) + \frac{\partial}{\partial x_j}[(\rho E + p)u_j] = 0 | ||
</math> | </math> | ||
| Line 28: | Line 28: | ||
* <math>p</math> is the pressure | * <math>p</math> is the pressure | ||
* <math>E</math> is the total energy per unit mass of fluid | * <math>E</math> is the total energy per unit mass of fluid | ||
| + | |||
| + | :<math> | ||
| + | E = \frac{p}{\gamma - 1} + \frac{1}{2} \rho |u|^2 | ||
| + | </math> | ||
| + | |||
| + | * <math>\gamma</math> is the [[ratio of specific heats]] | ||
| + | |||
| + | The above equations are closed by taking an equation of state, the simplest being the ideal gas | ||
| + | |||
| + | :<math> | ||
| + | p = \rho R T | ||
| + | </math> | ||
| + | |||
| + | where | ||
| + | |||
| + | * <math>R</math> is the gas constant | ||
| + | * <math>T</math> is the absolute temperature | ||
| + | |||
| + | ==Euler equations as the limit of Navier-Stokes equations== | ||
| + | |||
| + | Have a look at this discussion:<br> | ||
| + | http://www.cfd-online.com/Forum/fluent.cgi?read=32738 <br> | ||
| + | http://www.cfd-online.com/Forum/fluent.cgi?read=32788 | ||
| + | |||
| + | ==Related pages== | ||
| + | *[[Euler equations in conservation form]] | ||
| + | *[[Rotational invariance of Euler equations]] | ||
| + | *[[Inviscid flux jacobians]] | ||
Revision as of 04:38, 16 December 2005
A flow in which viscous effects can be neglected is known as inviscid flow. At high Reynolds numbers, flow past slender bodies involve thin boundary layers. Viscous effects are important only inside the boundary layer and the flow outside it is nearly inviscid. If the boundary layer is not separated then the inviscid flow model can be used to predict the pressure distribution with reasonable accuracy. Although no practical flow is inviscid, the inviscid assumption is valid if the time scales for diffusion are much larger compared to the time scales for convection, which is measured by the Reynolds number.
Governing Equations
The governing equations for inviscid flow, also known as Euler equations, are obtained by discarding the viscous terms from the Navier-Stokes equations
- Continuity equation
- Momentum equation
- Energy equation
where
-
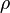 is the density
is the density
-
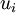 is the fluid velocity
is the fluid velocity
-
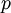 is the pressure
is the pressure
-
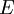 is the total energy per unit mass of fluid
is the total energy per unit mass of fluid
-
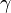 is the ratio of specific heats
is the ratio of specific heats
The above equations are closed by taking an equation of state, the simplest being the ideal gas
where
-
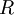 is the gas constant
is the gas constant
-
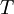 is the absolute temperature
is the absolute temperature
Have a look at this discussion:
http://www.cfd-online.com/Forum/fluent.cgi?read=32738
http://www.cfd-online.com/Forum/fluent.cgi?read=32788

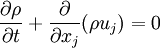
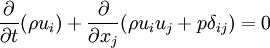
![\frac{\partial}{\partial t}(\rho E) + \frac{\partial}{\partial x_j}[(\rho E + p)u_j] = 0](/W/images/math/e/7/3/e73b09e7ac9cb3a2f73034d30bfbcb11.png)