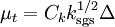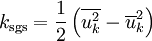Kinetic energy subgrid-scale model
From CFD-Wiki
(Difference between revisions)
m |
CrochIvare (Talk | contribs) (varlabascal) |
||
| Line 1: | Line 1: | ||
| + | libocacpa | ||
The subgrid-scale kinetic energy is defined as <br> | The subgrid-scale kinetic energy is defined as <br> | ||
:<math> k_{\rm sgs} = \frac{1}{2}\left(\overline{u_k^2} - \overline{u}_k^2 \right) </math> | :<math> k_{\rm sgs} = \frac{1}{2}\left(\overline{u_k^2} - \overline{u}_k^2 \right) </math> | ||
Revision as of 09:12, 17 December 2008
libocacpa
The subgrid-scale kinetic energy is defined as
The subgrid-scale stress can then be written as
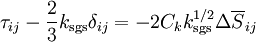
this gives us the transport equation for subgrid-scale kinetic energy
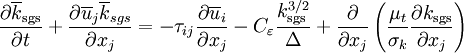
The subgrid-scale eddy viscosity,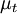 , is computed using
, is computed using 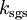 as
as