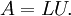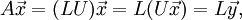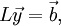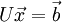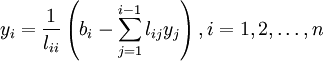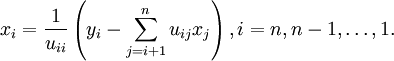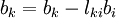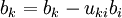LU decomposition
From CFD-Wiki
m (→Description) |
m (→Algorithm) |
||
| Line 35: | Line 35: | ||
: for k:=1 step until n do <br> | : for k:=1 step until n do <br> | ||
:: for i:=1 step until k-1 <br> | :: for i:=1 step until k-1 <br> | ||
| - | ::: <math>b_k=b_k- | + | ::: <math>b_k=b_k-l_{ki}b_{i}</math> <br> |
:: end loop (i) <br> | :: end loop (i) <br> | ||
| - | :: <math>b_{k}=b_{k}/ | + | :: <math>b_{k}=b_{k}/l_{kk}</math><br> |
: end loop (k) | : end loop (k) | ||
Backward substitution | Backward substitution | ||
: for k:=n stepdown until 1 do <br> | : for k:=n stepdown until 1 do <br> | ||
:: for i:=k+1 step until n <br> | :: for i:=k+1 step until n <br> | ||
| - | ::: <math>b_k=b_k- | + | ::: <math>b_k=b_k-u_{ki}b_{i}</math> <br> |
:: end loop (i) <br> | :: end loop (i) <br> | ||
| - | :: <math>x_{k}=b_{k}/ | + | :: <math>x_{k}=b_{k}/u_{kk}</math><br> |
: end loop (k) | : end loop (k) | ||
Revision as of 22:38, 18 December 2005
Description
Consider the system of equations 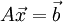 , where
, where 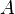 is an
is an 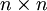 nonsingular matrix.
nonsingular matrix. 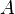 may be decomposed into an lower triangular part
may be decomposed into an lower triangular part 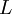 and an upper triangular part
and an upper triangular part 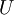 that will lead us to a direct procedure for the solution of the original system. This decomposition procedure is quite useful when more than one right-hand side (more than one
that will lead us to a direct procedure for the solution of the original system. This decomposition procedure is quite useful when more than one right-hand side (more than one 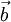 ) is to be used.
) is to be used.
The algorithm is relatively straightforward - first, we determine the upper and lower triangular parts:
Then,
where 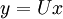 . Once we solve the system
. Once we solve the system
we will be able to find the solution to the original system by solving
The first solution is a foward substitution, while the second solution is a backward substitution. Both can be done efficiently once the factorization is available. The forward substitution may be expressed as
and the backward substitution process may be expressed as
Algorithm
Add factorization here
Forward substitution
- for k:=1 step until n do
- for i:=1 step until k-1
-
- end loop (i)
-
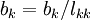
- for i:=1 step until k-1
- end loop (k)
Backward substitution
- for k:=n stepdown until 1 do
- for i:=k+1 step until n
-
- end loop (i)
-
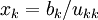
- for i:=k+1 step until n
- end loop (k)
Important Considerations
As with Gaussian elimination, LU decomposition is probably best used for relatively small, relatively non-sparse systems of equations (with small and non-sparse open to some interpretation). For larger and/or sparse problems, it would probably be best to either use an iterative method or use a direct solver package (e.g. DSCPACK) as opposed to writing one of your own.
If one has a single lefthand-side matrix and many right-hand side vectors, then LU decomposition would be a good solution procedure to consider. At the very least, it should be faster than solving each system separately with Gaussian elimination.