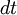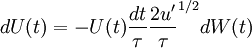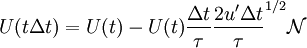Langevin equation
From CFD-Wiki
(Difference between revisions)
m |
|||
| Line 2: | Line 2: | ||
the Langevin equation is | the Langevin equation is | ||
:<math> | :<math> | ||
| - | dU(t) = - U(t) \frac{dt}{\tau} | + | dU(t) = - U(t) \frac{dt}{\tau} \frac{2 u'}{\tau}^{1/2} dW(t) |
</math> | </math> | ||
| Line 11: | Line 11: | ||
:<math> | :<math> | ||
| - | U(t | + | U(t \Delta t) = U(t) - U(t) \frac{\Delta t}{\tau} \frac{2 u' \Delta t}{\tau}^{1/2} \mathcal{N} |
</math> | </math> | ||
Revision as of 12:20, 15 June 2007
The stochastic differential equation (SDE) for velocity component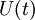 
,
the Langevin equation is
where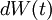 
is a Wiener process.
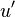is the turbulence intensity and 
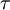a Lagrangian time-scale.
Th finite difference approximation of the above equation is
where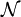 
is a standardized Gaussian random variable with 0 mean an unity variance
which is independent of 
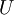on all other time steps (Pope 1994).
The Wiener process can be understood as Gaussian random variable with 0 mean
and variance 
