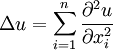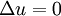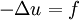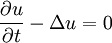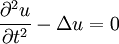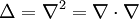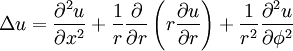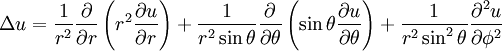Laplacian
From CFD-Wiki
| (4 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
The n-dimensional Laplacian operator in Cartesian coordinates is defined by | The n-dimensional Laplacian operator in Cartesian coordinates is defined by | ||
| - | <math> | + | :<math> |
\Delta u = \sum_{i=1}^n \frac{\partial^2 u}{\partial x_i^2} | \Delta u = \sum_{i=1}^n \frac{\partial^2 u}{\partial x_i^2} | ||
</math> | </math> | ||
| - | It is an important differential operator which occurs in many equations of mathematical physics and is usually associated with dissipative effects. Some of the important equations are | + | It is an important differential operator which occurs in many equations of mathematical physics and is usually associated with dissipative effects (except in the case of [[wave equation]]). Some of the important equations are |
| - | * Laplace equation | + | * [[Laplace equation]] |
| - | <math> | + | :<math> |
\Delta u = 0 | \Delta u = 0 | ||
</math> | </math> | ||
| - | * Poisson equation | + | * [[Poisson equation]] |
| - | <math> | + | :<math> |
| - | \Delta u = f | + | -\Delta u = f |
</math> | </math> | ||
| + | * [[Heat equation]] | ||
| + | |||
| + | :<math> | ||
| + | \frac{\partial u}{\partial t} - \Delta u = 0 | ||
| + | </math> | ||
| + | |||
| + | * [[Wave equation]] | ||
| + | |||
| + | :<math> | ||
| + | \frac{\partial^2 u}{\partial t^2} - \Delta u = 0 | ||
| + | </math> | ||
Solutions of these equations are very smooth and in most cases are infinitely differentiable (when the associated data of the problem are sufficiently smooth). | Solutions of these equations are very smooth and in most cases are infinitely differentiable (when the associated data of the problem are sufficiently smooth). | ||
| - | The Laplacian operator is invariant under coordinate rotation. | + | Folland (see reference below) explains the ubiquitous appearance of the Laplacian. |
| + | |||
| + | ''Why is it so ubiquitous ? The answer, which we shall prove, is that it commutes with translations and rotations and generates the ring of all differential operators with this property. Hence, the Laplacian is likely to turn up in the description of any physical process whose underlying physics is homogeneous (independent of position) and isotropic (independent of direction).'' | ||
| + | |||
| + | Moreover it can shown that any linear operator which commutes with translations and rotations must be a polynomial in <math>\Delta</math>, i.e., it must be of the form <math>\sum_j a_j \Delta^j</math> where the <math>a_j</math> are constants (see Folland). | ||
| + | |||
| + | The Laplacian operator is invariant under coordinate translation and rotation. | ||
| + | |||
| + | The Laplace operator is also denoted as <math>\nabla^2</math> since it is the divergence of the gradient operator | ||
| + | |||
| + | :<math> | ||
| + | \Delta = \nabla^2 = \nabla \cdot \nabla | ||
| + | </math> | ||
| + | |||
| + | == Laplacian in cylindrical coordinates == | ||
| + | |||
| + | If <math>(x,r,\phi)</math> are cylindrical coordinates, then the Laplacian of a scalar field variable <math>u</math> is | ||
| + | |||
| + | :<math> | ||
| + | \Delta u = \frac{\partial^2 u}{\partial x^2} + \frac{1}{r} \frac{\partial}{\partial r} \left( r \frac{\partial u}{\partial r} \right) + \frac{1}{r^2} \frac{\partial^2 u}{\partial \phi^2} | ||
| + | </math> | ||
| + | |||
| + | == Laplacian in spherical coordinates == | ||
| + | |||
| + | If <math>(r,\theta,\phi)</math> are spherical coordinates, then the Laplacian of a scalar field variable <math>u</math> is | ||
| + | |||
| + | :<math> | ||
| + | \Delta u = | ||
| + | \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial u}{\partial r} \right) + | ||
| + | \frac{1}{r^2 \sin\theta} \frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial u}{\partial \theta} \right) + | ||
| + | \frac{1}{r^2 \sin^2\theta} \frac{\partial^2 u}{\partial \phi^2} | ||
| + | </math> | ||
| + | |||
| + | == References == | ||
| + | |||
| + | * {{reference-book | author=Gerald B. Folland | year=1995 | title=Introduction to partial differential equations | rest=Princeton University Press}} | ||
Latest revision as of 08:19, 12 April 2007
The n-dimensional Laplacian operator in Cartesian coordinates is defined by
It is an important differential operator which occurs in many equations of mathematical physics and is usually associated with dissipative effects (except in the case of wave equation). Some of the important equations are
Solutions of these equations are very smooth and in most cases are infinitely differentiable (when the associated data of the problem are sufficiently smooth).
Folland (see reference below) explains the ubiquitous appearance of the Laplacian.
Why is it so ubiquitous ? The answer, which we shall prove, is that it commutes with translations and rotations and generates the ring of all differential operators with this property. Hence, the Laplacian is likely to turn up in the description of any physical process whose underlying physics is homogeneous (independent of position) and isotropic (independent of direction).
Moreover it can shown that any linear operator which commutes with translations and rotations must be a polynomial in 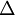 , i.e., it must be of the form
, i.e., it must be of the form 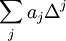 where the
where the 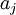 are constants (see Folland).
are constants (see Folland).
The Laplacian operator is invariant under coordinate translation and rotation.
The Laplace operator is also denoted as 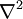 since it is the divergence of the gradient operator
since it is the divergence of the gradient operator
Laplacian in cylindrical coordinates
If 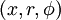 are cylindrical coordinates, then the Laplacian of a scalar field variable
are cylindrical coordinates, then the Laplacian of a scalar field variable 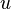 is
is
Laplacian in spherical coordinates
If 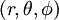 are spherical coordinates, then the Laplacian of a scalar field variable
are spherical coordinates, then the Laplacian of a scalar field variable 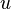 is
is
References
- Gerald B. Folland (1995), Introduction to partial differential equations, Princeton University Press.