Laplacian
From CFD-Wiki
The n-dimensional Laplacian operator in Cartesian coordinates is defined by
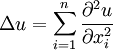
It is an important differential operator which occurs in many equations of mathematical physics and is usually associated with dissipative effects. Some of the important equations are
- Laplace equation
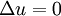
- Poisson equation
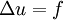
Solutions of these equations are very smooth and in most cases are infinitely differentiable (when the associated data of the problem are sufficiently smooth).
The Laplacian operator is invariant under coordinate rotation.
