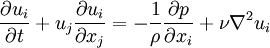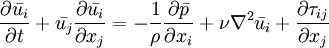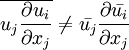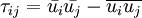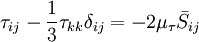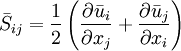Large eddy simulation (LES)
From CFD-Wiki
m (Large eddy simulations (LES) moved to Large eddy simulation (LES)) |
Discoganya (Talk | contribs) (Added some introduction and showed the derivation of the main equations) |
||
| Line 1: | Line 1: | ||
| - | The | + | Large eddy simulation (LES) is a popular technique for simulating turbulent flows. A common deduction of [[Kolmogorov]]'s (1941) theory of self similarity is that the large eddies of the flow are dependant on the geometry while the smaller scales more [[universal]]. This feature allows one to explicitly solve for the large eddies in a calculation and implicitly account for the small eddies by using a [[sub-grid scale model]] (SGS model). |
| + | |||
| + | Mathematically, one may think of separating the velocity field into a resolved and sub-grid part. The resolved part of the field represent the "large" eddies, while the sub-grid part of the velocity represent the "small scales" whose effect on the resolved field is included through the sub-grid scale model. Formally, one may think of filtering as the convolution of a function with a [[LES filters|filtering kernel]]. However, most practical (and commercial) implimentations of LES, use the grid itself as the filter, and perform no explicit filtering. More information about the theory and application of filters is found [[LES filters|here]]. | ||
| + | |||
| + | This page is mainly focused on LES of incompressible flows. For compressible flows, see [[Favre averaged Navier-Stokes equations]]. | ||
| + | |||
| + | Typically, one would begin with the incompressible [[Navier-Stokes equations]] of motion, <br> | ||
| + | :<math> | ||
| + | \frac{\partial{u_i}}{\partial t} + u_j \frac{\partial u_i}{\partial x_j} = -\frac{1}{\rho} \frac{\partial p}{\partial x_i} + \nu \nabla^2 u_i | ||
| + | </math> | ||
| + | |||
| + | and by the application of a filtering kernel, derive the equations of motion for the resolved field, | ||
| + | |||
| + | :<math> | ||
| + | \frac{\partial{\bar{u_i}}}{\partial t} + \bar{u_j} \frac{\partial \bar{u_i}}{\partial x_j} = -\frac{1}{\rho} \frac{\partial \bar{p}}{\partial x_i} + \nu \nabla^2 \bar{u_i} | ||
| + | + \frac{\partial \tau_{ij}}{\partial x_j} | ||
| + | </math> | ||
| + | |||
| + | Velocities and pressures with an overbar denote the resolved field after the application of the filtering operation. Similar equations can be derived for the sub-grid scale field (i.e. the residual field). An extra term <math> \frac{\partial \tau_{ij}}{\partial x_j} </math> arises from the non-linear advection terms, due to the fact that | ||
| + | :<math> | ||
| + | \overline{ u_j \frac{\partial u_i}{\partial x_j} } \ne | ||
| + | \bar{u_j} \frac{\partial \bar{u_i}}{\partial x_j} | ||
| + | </math> | ||
| + | |||
| + | and hence | ||
| + | :<math> | ||
| + | \tau_{ij} = \bar{u_i} \bar{u_j} - \overline{u_i u_j} | ||
| + | </math> | ||
| + | |||
| + | Subgrid-scale turbulence models usually employ the [[Boussinesq hypothesis]], and seek to calculate (the deviatoric part of) the SGS stress using: <br> | ||
:<math> | :<math> | ||
| - | \tau _{ij} - \frac{1}{3}\tau _{kk} \delta _{ij} = - 2\mu | + | \tau _{ij} - \frac{1}{3}\tau _{kk} \delta _{ij} = - 2\mu _\tau \bar S_{ij} |
</math> | </math> | ||
| Line 12: | Line 41: | ||
</math> | </math> | ||
<br> | <br> | ||
| - | and <math> \mu | + | and <math> \mu _\tau </math> is the subgrid-scale turbulent viscosity. |
Revision as of 17:38, 18 September 2005
Large eddy simulation (LES) is a popular technique for simulating turbulent flows. A common deduction of Kolmogorov's (1941) theory of self similarity is that the large eddies of the flow are dependant on the geometry while the smaller scales more universal. This feature allows one to explicitly solve for the large eddies in a calculation and implicitly account for the small eddies by using a sub-grid scale model (SGS model).
Mathematically, one may think of separating the velocity field into a resolved and sub-grid part. The resolved part of the field represent the "large" eddies, while the sub-grid part of the velocity represent the "small scales" whose effect on the resolved field is included through the sub-grid scale model. Formally, one may think of filtering as the convolution of a function with a filtering kernel. However, most practical (and commercial) implimentations of LES, use the grid itself as the filter, and perform no explicit filtering. More information about the theory and application of filters is found here.
This page is mainly focused on LES of incompressible flows. For compressible flows, see Favre averaged Navier-Stokes equations.
Typically, one would begin with the incompressible Navier-Stokes equations of motion,
and by the application of a filtering kernel, derive the equations of motion for the resolved field,
Velocities and pressures with an overbar denote the resolved field after the application of the filtering operation. Similar equations can be derived for the sub-grid scale field (i.e. the residual field). An extra term 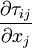 arises from the non-linear advection terms, due to the fact that
arises from the non-linear advection terms, due to the fact that
and hence
Subgrid-scale turbulence models usually employ the Boussinesq hypothesis, and seek to calculate (the deviatoric part of) the SGS stress using:
where 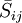 is the rate-of-strain tensor for the resolved scale defined by
is the rate-of-strain tensor for the resolved scale defined by
and 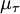 is the subgrid-scale turbulent viscosity.
is the subgrid-scale turbulent viscosity.