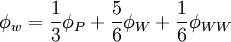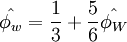Linear Schemes - structured grids
From CFD-Wiki
(→QUICK - Quadratic Upwind Interpolation for Convective Kinematics (also UDS-3 or QUDS)) |
(→CUDS - Cubic Upwind Difference Scheme (also CUS or UDS-4)) |
||
| Line 78: | Line 78: | ||
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
:<math> | :<math> | ||
| - | + | \phi_{w}=\frac{1}{3}\phi_{P} + \frac{5}{6}\phi_{W} + \frac{1}{6}\phi_{WW} | |
</math> | </math> | ||
</td><td width="5%">(2)</td></tr></table> | </td><td width="5%">(2)</td></tr></table> | ||
| Line 86: | Line 86: | ||
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
:<math> | :<math> | ||
| - | \hat{ | + | \hat{\phi_{w}}=\frac{1}{3} + \frac{5}{6}\hat{\phi_{W}} |
</math> | </math> | ||
</td><td width="5%">(2)</td></tr></table> | </td><td width="5%">(2)</td></tr></table> | ||
Revision as of 11:18, 29 October 2005
SOU - Second Order Upwind (also LUDS or UDS-2)
S.P.Vanka ({{{year}}}), "Second-order upwind differencing ina recirculating flow", AIAA J., 25, 1435-1441.
R.F.Warming and R.M. Beam (1976), "Upwind second order difference schemes and applications in aerodynamics flows", AIAA J. 14 (1976) 1241-1249.
Skew - Upwind
G.D.Raithby , Skew upstream differencing schemes for problems involving fluid flow, Computational Methods Applied Mech. Engineering, 9, 153-164 (1976)
QUICK - Quadratic Upwind Interpolation for Convective Kinematics (also UDS-3 or QUDS)
B.P.Leonard, A stable and accurate modelling procedure based on quadratic interpolation, Comput. Methods Appl. Mech. Engrg. 19 (1979) 58-98
Usual variables
|
| (2) |
|
| (2) |
Normalised variables (uniform grid)
|
| (2) |
Normalised variables (non-uniform grid)
|
| (2) |
|
| (2) |
LUS - Linear Upwind Scheme
H.C.Price, R.S. Varga and J.E.Warren , Application of oscillation matrices to diffusion-convection equations, Journal Math. and Phys., Vol. 45, p.301, (1966)
Fromm - Fromm's Upwind Scheme
CUDS - Cubic Upwind Difference Scheme (also CUS or UDS-4)
In CUDS (UDS-4) for interpolation of function is used three upwind nodes and one node downstream.
usual variables
|
| (2) |
normalised variables (uniform grids)
|
| (2) |
R.K. Aragval
A third-order-accurate upwind scheme for Navier-Stokes solution at high Reynolds numbers
Paper No. AIAA-81-0112, AIAA 19th Aerospace Science Meeting, St. Louis, 1982.
CUI - Cubic Upwind Interpolation
B.P. Leonard
A survey of finite differences of opinion on numerical muddling of incompressible defective confusion equation
paper in ASME, Applied Mechanics Division, Winter Annual Meeting, 1979
Return to Numerical Methods
Return to Approximation Schemes for convective term - structured grids

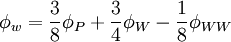
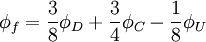
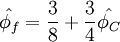
![\begin{matrix}
\hat{\phi_{w}} & = \left\{ \left( 1 + C_{1} \right) \left( 1 - C_{2} \right)\hat{\phi_{W}} + C_{2} \left[ 1 - \frac{C_{1} \left( 1 - C_{2} \right) }{ C_{1} + C_{2} } \right] \right\} U^{+}_{w} + \\
+ & \left\{ C_{2} \left( 1 + C_{3} \right) \hat{\phi_{P}} + \left( 1 - C_{2} \right) \left[ 1 - \frac{C_{2} C_{3} }{ 1- C_{2} + C_{3} } \right] \right\} U^{-}_{w}
\end{matrix}](/W/images/math/9/2/5/925db1d1d212b7ae8fecb9ac1cf4a7ef.png)
![\begin{matrix}
\hat{\phi_{f}} & = \left\{ \left( 1 + C_{1} \right) \left( 1 - C_{2} \right)\hat{\phi_{C}} + C_{2} \left[ 1 - \frac{C_{1} \left( 1 - C_{2} \right) }{ C_{1} + C_{2} } \right] \right\} U^{+}_{f} + \\
+ & \left\{ C_{2} \left( 1 + C_{3} \right) \hat{\phi_{D}} + \left( 1 - C_{2} \right) \left[ 1 - \frac{C_{2} C_{3} }{ 1- C_{2} + C_{3} } \right] \right\} U^{-}_{f}
\end{matrix}](/W/images/math/0/b/8/0b89df8d7877d9716eaa0ea033f8d368.png)