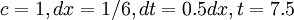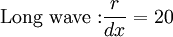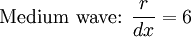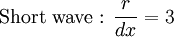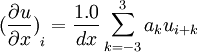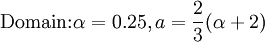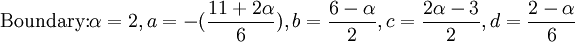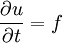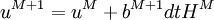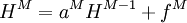Linear wave propagation
From CFD-Wiki
m (Reverted edits by CnadeLcelt (Talk) to last version by Rangan86) |
|||
| (5 intermediate revisions not shown) | |||
| Line 11: | Line 11: | ||
== Exact solution == | == Exact solution == | ||
| - | :<math> u(x, | + | :<math> u(x,t)=exp[-ln(2){(\frac{x-x_c-ct}{r})}^2]</math> |
| + | |||
== Numerical method == | == Numerical method == | ||
:<math>c=1,dx=1/6,dt=0.5dx,t=7.5</math> | :<math>c=1,dx=1/6,dt=0.5dx,t=7.5</math> | ||
| Line 20: | Line 21: | ||
==== Explicit Scheme (DRP)==== | ==== Explicit Scheme (DRP)==== | ||
:<math> {(\frac{\partial u}{\partial x})}_i=\frac{1.0}{dx}\sum_{k=-3}^3 a_k u_{i+k} </math> | :<math> {(\frac{\partial u}{\partial x})}_i=\frac{1.0}{dx}\sum_{k=-3}^3 a_k u_{i+k} </math> | ||
| - | The coefficients can be found in Tam( | + | The coefficients can be found in Tam(1993).At the right boundaries use fourth order central difference and fourth backward difference.At left boundaries use second order central difference for i=2 and fourth order central difference for i=3.The Dispersion relation preserving (DRP) finite volume scheme can be found in Popescu (2005). |
====Implicit Scheme(Compact)==== | ====Implicit Scheme(Compact)==== | ||
:Domain: <math>\alpha v_{i-1} + v_i + \alpha v_{i+1}=\frac{a}{2h}(u_{i+1}-u_{i-1}) </math> | :Domain: <math>\alpha v_{i-1} + v_i + \alpha v_{i+1}=\frac{a}{2h}(u_{i+1}-u_{i-1}) </math> | ||
:Boundaries: <math> v_1+\alpha v_2=\frac{1}{h}(au_1+bu_2+cu_3+du_4) </math> | :Boundaries: <math> v_1+\alpha v_2=\frac{1}{h}(au_1+bu_2+cu_3+du_4) </math> | ||
where v refers to the first derivative.For a general treatment of compact scheme refer to Lele (1992).In this test case the following values are used | where v refers to the first derivative.For a general treatment of compact scheme refer to Lele (1992).In this test case the following values are used | ||
| - | :<math> \mbox{Domain} \alpha=0.25 , a=\frac{2}{3}(\alpha+2) </math> | + | :<math> \mbox{Domain:} \alpha=0.25 , a=\frac{2}{3}(\alpha+2) </math> |
| - | :<math> \mbox{Boundary} \alpha=2 ,a=-(\frac{11+2\alpha}{6}),b=\frac{6-\alpha}{2},c=\frac{2\alpha-3}{2},d=\frac{2-\alpha}{6} </math> | + | :<math> \mbox{Boundary:} \alpha=2 ,a=-(\frac{11+2\alpha}{6}),b=\frac{6-\alpha}{2},c=\frac{2\alpha-3}{2},d=\frac{2-\alpha}{6} </math> |
| + | Both the schemes are 4th order accurate in the domain.The compact scheme has third order accuracy at the boundary. | ||
| + | ===Time (4th Order Runga-Kutta)=== | ||
| + | :<math>\frac{\partial u}{\partial t}=f </math> | ||
| - | = | + | :<math>u^{M+1} =u^M + b^{M+1}dtH^M </math> |
| + | :<math> H^M=a^MH^{M-1}+f^M </math> | ||
| + | ,M=1,2..5 .The coefficients a and b can be found in Williamson(1980) | ||
| + | |||
| + | == Results == | ||
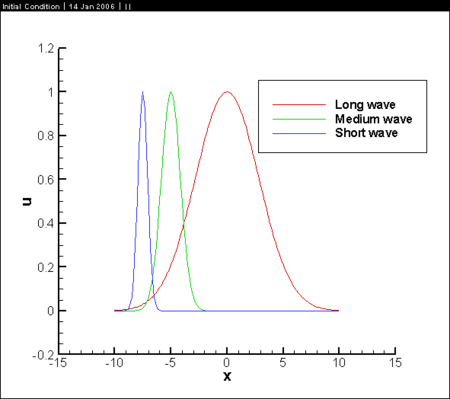
[[Image:Initial_condition.png|450px]] | [[Image:Initial_condition.png|450px]] | ||
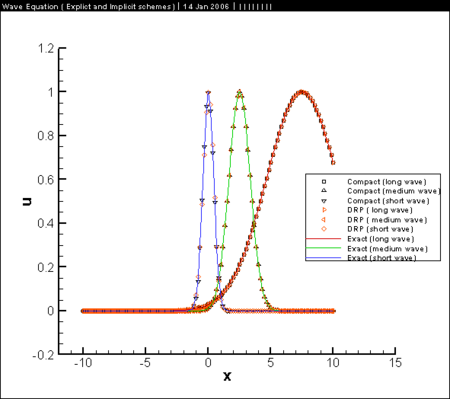
[[Image:Result_wave.png|450px]] | [[Image:Result_wave.png|450px]] | ||
== Reference == | == Reference == | ||
| + | {{reference-paper|author=Mihaela Popescu, Wei Shyy , Marc Garbey|year=2005|title=Finite volume treatment of dispersion-relation-preserving and optimized prefactored compact schemes for wave propagation|rest=Journal of Computational Physics, Vol. 210, pp. 705-729}} | ||
| + | |||
| + | {{reference-paper|author=Tam and Webb|year=1993|title=Dispersion-relation-preserving finite difference schemes for computational acoustics|rest=Journal of Computational Physics, Vol. 107, pp. 262-281}} | ||
| + | |||
| + | {{reference-paper|author=SK Lele|year=1992|title=Compact finite difference schemes with spectrum-like resolution|rest=Journal of Computational Physics, Vol.103, pp.16-42}} | ||
| + | |||
| + | {{reference-paper|author=Williamson|year=1980|title=Low Storage Runge-Kutta Schemes|rest=Journal of Computational Physics, Vol.35, pp.48–56}} | ||
Latest revision as of 09:55, 17 December 2008
Contents |
Problem definition
Domain
Initial Condition
Boundary condition
Exact solution
Numerical method
Space
Explicit Scheme (DRP)
The coefficients can be found in Tam(1993).At the right boundaries use fourth order central difference and fourth backward difference.At left boundaries use second order central difference for i=2 and fourth order central difference for i=3.The Dispersion relation preserving (DRP) finite volume scheme can be found in Popescu (2005).
Implicit Scheme(Compact)
- Domain:
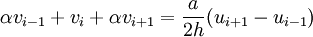
- Boundaries:
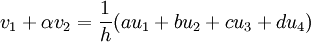
where v refers to the first derivative.For a general treatment of compact scheme refer to Lele (1992).In this test case the following values are used
Both the schemes are 4th order accurate in the domain.The compact scheme has third order accuracy at the boundary.
Time (4th Order Runga-Kutta)
,M=1,2..5 .The coefficients a and b can be found in Williamson(1980)
Results
Reference
Mihaela Popescu, Wei Shyy , Marc Garbey (2005), "Finite volume treatment of dispersion-relation-preserving and optimized prefactored compact schemes for wave propagation", Journal of Computational Physics, Vol. 210, pp. 705-729.
Tam and Webb (1993), "Dispersion-relation-preserving finite difference schemes for computational acoustics", Journal of Computational Physics, Vol. 107, pp. 262-281.
SK Lele (1992), "Compact finite difference schemes with spectrum-like resolution", Journal of Computational Physics, Vol.103, pp.16-42.
Williamson (1980), "Low Storage Runge-Kutta Schemes", Journal of Computational Physics, Vol.35, pp.48–56.

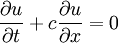
![x=[-10,10]](/W/images/math/1/b/1/1b14c536c4db5da52bbdcfe07f70db81.png)
![u(x,0)=exp[-ln(2){(\frac{x-x_c}{r})}^2]](/W/images/math/b/3/8/b38fab63c854b1f256b78d925988a116.png)
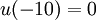
![u(x,t)=exp[-ln(2){(\frac{x-x_c-ct}{r})}^2]](/W/images/math/7/2/5/7251cf8065ea79bae8a05b09974b36ba.png)