Meshing
From CFD-Wiki
m |
|||
| (9 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | {{Meshing table of contents}} | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
==Introduction== | ==Introduction== | ||
| - | + | The partial differential equations that govern fluid flow and heat transfer are not usually amenable to analytical solutions, except for very simple cases. Therefore, in order to analyze fluid flows, flow domains are split into smaller subdomains (made up of geometric primitives like hexahedra and tetrahedra in 3D and quadrilaterals and triangles in 2D). The governing equations are then discretized and solved inside each of these subdomains. Typically, one of three methods is used to solve the approximate version of the system of equations: finite volumes, finite elements, or finite differences. Care must be taken to ensure proper continuity of solution across the common interfaces between two subdomains, so that the approximate solutions inside various portions can be put together to give a complete picture of fluid flow in the entire domain. The subdomains are often called elements or cells, and the collection of all elements or cells is called a mesh or grid. The origin of the term mesh (or grid) goes back to early days of CFD when most analyses were 2D in nature. For 2D analyses, a domain split into elements resembles a wire mesh, hence the name. | |
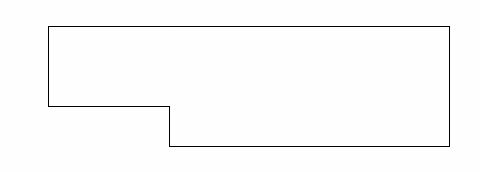
An example of a 2D analysis domain (flow over a backward facing step) and its mesh are shown in pictures below. | An example of a 2D analysis domain (flow over a backward facing step) and its mesh are shown in pictures below. | ||
Latest revision as of 09:15, 3 January 2012
| Introduction |
| Mesh classification |
| Structured mesh generation |
| Unstructured mesh generation |
| Special topics |
Introduction
The partial differential equations that govern fluid flow and heat transfer are not usually amenable to analytical solutions, except for very simple cases. Therefore, in order to analyze fluid flows, flow domains are split into smaller subdomains (made up of geometric primitives like hexahedra and tetrahedra in 3D and quadrilaterals and triangles in 2D). The governing equations are then discretized and solved inside each of these subdomains. Typically, one of three methods is used to solve the approximate version of the system of equations: finite volumes, finite elements, or finite differences. Care must be taken to ensure proper continuity of solution across the common interfaces between two subdomains, so that the approximate solutions inside various portions can be put together to give a complete picture of fluid flow in the entire domain. The subdomains are often called elements or cells, and the collection of all elements or cells is called a mesh or grid. The origin of the term mesh (or grid) goes back to early days of CFD when most analyses were 2D in nature. For 2D analyses, a domain split into elements resembles a wire mesh, hence the name.
An example of a 2D analysis domain (flow over a backward facing step) and its mesh are shown in pictures below.
The process of obtaining an appropriate mesh (or grid) is termed mesh generation (or grid generation), and has long been considered a bottleneck in the analysis process due to the lack of a fully automatic mesh generation procedure. Specialized software progams have been developed for the purpose of mesh and grid generation, and access to a good software package and expertise in using this software are vital to the success of a modeling effort.
|| Introduction | Mesh Classification >>