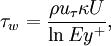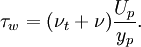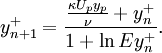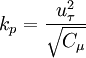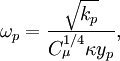Near-wall treatment for k-omega models
From CFD-Wiki
| Line 45: | Line 45: | ||
which are the values for <math>k</math> and <math>\omega</math> according to Wilcox2006 asymptotic analysis of log layer. These wall functions for <math>k</math> and <math>\omega</math> are the results of the solution of model equation for the logarithmic layer. | which are the values for <math>k</math> and <math>\omega</math> according to Wilcox2006 asymptotic analysis of log layer. These wall functions for <math>k</math> and <math>\omega</math> are the results of the solution of model equation for the logarithmic layer. | ||
| - | The above methodology is known to produce spurious results in separated flows, where, by definition, <math>u_\tau = 0</math>. Many extension of this approach has been proposed. | + | The above methodology is known to produce spurious results in separated flows, where, by definition, <math>u_\tau = 0</math> at the separation and reattachment point. Many extension of this approach has been proposed. |
Revision as of 12:23, 31 October 2011
Standard wall function approach
There are two possible ways of implementing wall functions in a finite volume code:
- Additional source term in the momentum equations.
- Modification of turbulent viscosity in cells adjacent to solid walls.
The source term in the first approach is simply the difference between logarithmic and linear interpolation of velocity gradient multiplied by viscosity (the difference between shear stresses). The second approach does not attempt to reproduce the correct velocity gradient. Instead, turbulent viscosity is modified in such a way as to guarantee the correct shear stress.
Using the compact version of log-law
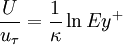 | (1) |
where 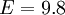 is equivalent to additive constants, and and using
is equivalent to additive constants, and and using 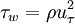 we obtain:
we obtain:
On the other hand, the linear interpolation for shear stress, rembembering that 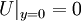 , is:
, is:
Comparing the above equations we obtain an expression for turbulent viscosity can be obtained:
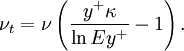 | (2) |
Note that 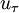 has been been incorporated in
has been been incorporated in 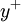 . The latter remains the only unknown in the equation and has to be estimated for the current velocity field. In the standard approach this cannot be done explicitly and instead an implicit way of obtaining
. The latter remains the only unknown in the equation and has to be estimated for the current velocity field. In the standard approach this cannot be done explicitly and instead an implicit way of obtaining 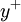 has to be employed.
has to be employed.
After multiplying log law (1) by 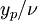 and after reorganising some terms we get:
and after reorganising some terms we get:
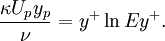 | (3) |
This equation can be solved numerically with respect to 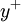 for example via root searching algorithms e.g. Newton method for specified
for example via root searching algorithms e.g. Newton method for specified 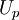 ,
, 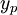 and
and 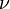 . One iteration in a Newton method for (3) is
. One iteration in a Newton method for (3) is
Thus obtained 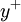 is then substituted to (2) Eventually the estimated
is then substituted to (2) Eventually the estimated 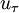 serves also to define the values of turbulent quantities in the cell adjacent to the wall:
serves also to define the values of turbulent quantities in the cell adjacent to the wall:
which are the values for  and
and 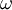 according to Wilcox2006 asymptotic analysis of log layer. These wall functions for
according to Wilcox2006 asymptotic analysis of log layer. These wall functions for  and
and 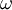 are the results of the solution of model equation for the logarithmic layer.
are the results of the solution of model equation for the logarithmic layer.
The above methodology is known to produce spurious results in separated flows, where, by definition, 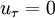 at the separation and reattachment point. Many extension of this approach has been proposed.
at the separation and reattachment point. Many extension of this approach has been proposed.
FLUENT
Both k- omega models (std and sst) are available as low-Reynolds-number models as well as high-Reynolds-number models.
The wall boundary conditions for the k equation in the k- omega models are treated in the same way as the k equation is treated when enhanced wall treatments are used with the k- epsilon models.
This means that all boundary conditions for
- wall-function meshes will correspond to the wall function approach, while for the
- fine meshes, the appropriate low-Reynolds-number boundary conditions will be applied.
In Fluent, that means:
If the Transitional Flows option is enabled in the Viscous Model panel, low-Reynolds-number variants will be used, and, in that case, mesh guidelines should be the same as for the enhanced wall treatment
(y+ at the wall-adjacent cell should be on the order of y+ = 1. However, a higher y+ is acceptable as long as it is well inside the viscous sublayer (y+ < 4 to 5).)
If Transitional Flows option is not active, then the mesh guidelines should be the same as for the wall functions.
(For [...] wall functions, each wall-adjacent cell's centroid should be located within the log-law layer, 30 < y+ < 300. A y+ value close to the lower bound y+ = 30 is most desirable.)
Reference:
FLUENT 6.2 Documentation, 2006