CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > RNG-LES model

RNG-LES model

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
Line 3: Line 3:
\mu _{eff}  = \mu \left[ {1 + H\left( x \right)} \right]^{1/3}
\mu _{eff}  = \mu \left[ {1 + H\left( x \right)} \right]^{1/3}
</math> . <br>
</math> . <br>
-
Where <math> H\left( x \right) </math> is given by: <br>
+
The function <math> H\left( x \right) </math> is defined as: <br>
:<math>
:<math>
Line 29: Line 29:
:<math>  
:<math>  
\mu _s  = \rho \left[ {C_{rng}} Vol^{1/3} \right]^{2} \begin{vmatrix} S \end{vmatrix}  
\mu _s  = \rho \left[ {C_{rng}} Vol^{1/3} \right]^{2} \begin{vmatrix} S \end{vmatrix}  
 +
</math>
 +
<br>
 +
Where <math> C_{rng}  </math> is given by <br>
 +
:<math>
 +
{C_{rng}  = 0.157}
</math>
</math>

Revision as of 08:23, 13 September 2005

Based on Renormalization Group Theory. Here \mu _{eff} = \mu \left[ {1 + H\left( x \right)} \right]^{1/3} .
The function 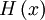H\left( x \right) is defined as:

H\left( x \right) \begin{matrix} = x \begin{matrix} {} & ; & {x > 0} \\ \end{matrix} \\ = 0 \begin{matrix} {} & ; & {x \le 0} \\ \end{matrix} \end{matrix}


x is given by 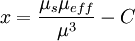x = {{\mu _s \mu _{eff} } \over {\mu ^3 }} - C

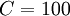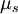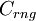Where {C = 100} and \mu _s is given by:

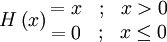
\mu _s = \rho \left[ {C_{rng}} Vol^{1/3} \right]^{2} \begin{vmatrix} S \end{vmatrix}


Where C_{rng} is given by

{C_{rng} = 0.157}
Retrieved from "https://www.cfd-online.com/Wiki/RNG-LES_model"
My wiki