SIMPLE algorithm
From CFD-Wiki
SIMPLE [Semi-Implicit Method for Pressure-Linked Equations]
If a steady-state problem is being solved iteratively, it is not necessary to fully resolve the linear pressure-velocity coupling, as the changes between consecutive solutions are no longer small. The SIMPLE algorithm:
- An approximation of the velocity field is obtained by solving the momentum equation. The pressure gradient term is calculated using the pressure distribution from the previous iteration or an initial guess.
- The pressure equation is formulated and solved in order to obtain the new pressure distribution.
- Velocities are corrected and a new set of conservative fluxes is calculated.
SIMPLE Solver Algorithm
The algorithm may be summarized as follows:
The basic steps in the solution update are as follows:
- Set the boundary conditions.
- Compute the gradients of velocity and pressure.
- Solve the discretized momentum equation to compute the intermediate velocity field .
- Compute the uncorrected mass fluxes at faces .
- Solve the pressure correction equation to produce cell values of the pressure correction .
- Update the pressure field:
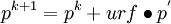 where urf is the under-relaxation factor for pressure.
where urf is the under-relaxation factor for pressure.
- Update the boundary pressure corrections
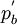 .
.
- Correct the face mass fluxes:
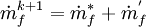
- Correct the cell velocities:
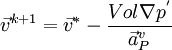 ; where
; where 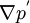 is the gradient of the pressure corrections,
is the gradient of the pressure corrections, 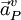 is the vector of central coefficients for the discretized linear system representing the velocity equation and Vol is the cell volume.
is the vector of central coefficients for the discretized linear system representing the velocity equation and Vol is the cell volume.
- Update density due to pressure changes.
Sample code for solving Lid-Driven_cavity test (Re=1000) - Fortran 90
References
- Patankar, S. V. and Spalding, D.B. (1972), "A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows", Int. J. of Heat and Mass Transfer, Volume 15, Issue 10, October 1972, Pages 1787-1806.
Return to Numerical Methods
