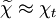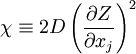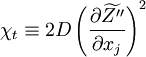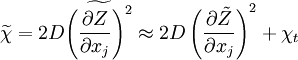Scalar dissipation
From CFD-Wiki
m (fixed case) |
m |
||
| Line 21: | Line 21: | ||
Opposite to the kinetic energy dissipation, most of the scalar dissipation occur at the finest scales. | Opposite to the kinetic energy dissipation, most of the scalar dissipation occur at the finest scales. | ||
| - | In [[Conditional | + | In [[Conditional Moment Closure (CMC)]] and [[Flamelet based on conserved scalar ]] models, the quantity of interest |
is the " main scalar dissipation rate", <math> \widetilde{\chi} </math>. From Favre Averaging the laminar | is the " main scalar dissipation rate", <math> \widetilde{\chi} </math>. From Favre Averaging the laminar | ||
dissipation rate | dissipation rate | ||
Revision as of 17:09, 31 January 2006
Scalar dissipation is a very important quantity in non-premixed combustion modelling. It often provides the connection between the mixing field and the combustion modelling. It is specially important in flamelet and RANS models.
In a laminar flow the scalar dissipation rate is defined (units are 1/s) as
where 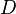 is the diffusion coefficient of the scalar.
is the diffusion coefficient of the scalar.
In turbulent flows, the scalar dissipation is seen as a scalar energy dissipation} and its role is to
destroy (dissipate) scalar variance (scalar energy) analogous to the dissipation of the
turbulent energy  . This term is known as the turbulent scalar dissipation
and is written as
. This term is known as the turbulent scalar dissipation
and is written as
Opposite to the kinetic energy dissipation, most of the scalar dissipation occur at the finest scales.
In Conditional Moment Closure (CMC) and Flamelet based on conserved scalar models, the quantity of interest
is the " main scalar dissipation rate", 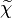 . From Favre Averaging the laminar
dissipation rate
. From Favre Averaging the laminar
dissipation rate
Under RANS assumptions gradient of the scalar fluctuations are much larger than gradients of the means,
and therefore the mean scalar dissipation rate is approximately the turbulent dissipation rate