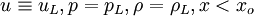Shock tube problem
From CFD-Wiki
(Difference between revisions)
| Line 3: | Line 3: | ||
:<math> u\equiv u_R ,p=p_R,\rho=\rho_R,x>x_o </math> | :<math> u\equiv u_R ,p=p_R,\rho=\rho_R,x>x_o </math> | ||
where <math> p_L>p_R </math> diaphragm being located at <math> x=x_o </math> | where <math> p_L>p_R </math> diaphragm being located at <math> x=x_o </math> | ||
| + | |||
| + | Two cases are considered and the flow is simulated using Roe first-order scheme and Steger-Warming vector splitting scheme. | ||
| + | |||
| + | :Case 1 <math> p_R \equiv 1.2*10^4 Pa,p_L=10^5 Pa,u_L=u_R=0,\rho_R=0.125,\rho_L=1.0 kg/m^3 ,x_o=5 m ,t_f=0.0061 s </math> | ||
| + | :Case 2 <math> p_R \equiv 1.2*10^3 Pa,p_L=10^5 Pa,u_L=u_R=0,\rho_R=0.01,\rho_L=1.0 kg/m^3 ,x_o=5 m ,t_f=0.0039 s </math> | ||
| + | |||
| + | The computational domain is <math> [0,2x_o] </math>.The boundary conditions are set equal to the intial conditions of the undisturbed gas.The computations are carried out with 600 grid points. | ||
Revision as of 04:30, 21 September 2005
The test case involves the 1-D Euler equation describing the flow.The initial condition is given by
where  diaphragm being located at
diaphragm being located at 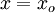
Two cases are considered and the flow is simulated using Roe first-order scheme and Steger-Warming vector splitting scheme.
- Case 1
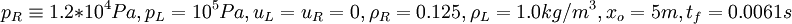
- Case 2
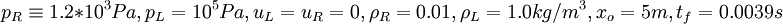
The computational domain is ![[0,2x_o]](/W/images/math/a/1/7/a17aaab58beb4ddf38dd1f34a33e92de.png) .The boundary conditions are set equal to the intial conditions of the undisturbed gas.The computations are carried out with 600 grid points.
.The boundary conditions are set equal to the intial conditions of the undisturbed gas.The computations are carried out with 600 grid points.