Skin friction coefficient
From CFD-Wiki
m |
m |
||
| Line 23: | Line 23: | ||
:<math>C_f = 0.370 \, [ log_{10}(Re_x) ]^{-2.584} </math> | :<math>C_f = 0.370 \, [ log_{10}(Re_x) ]^{-2.584} </math> | ||
| - | (equation 38 in [[#References|[ | + | (equation 38 in [[#References|[1]]]): |
:<math>1.0/C_f^{1/2} = 1.7 + 4.15 \, log_{10} (Re_x \, C_f) </math> | :<math>1.0/C_f^{1/2} = 1.7 + 4.15 \, log_{10} (Re_x \, C_f) </math> | ||
Revision as of 19:38, 22 September 2011
The skin friction coefficient, 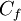 , is defined by:
, is defined by:
Where 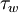 is the local wall shear stress,
is the local wall shear stress, 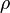 is the fluid density and
is the fluid density and 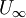 is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet).
is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet).
For a turbulent boundary layer several approximation formulas for the local skin friction for a flat plate can be used:
1/7 power law:
1/7 power law with experimental calibration (equation 21.12 in [1]):
Schlichting (equation 21.16 footnote in [3])
Schultz-Grunov (equation 21.19a in [3]):
(equation 38 in [1]):
The following skin friction formulas are extracted from [2],p.19. Proper reference needed:
Prandtl (1927):
Telfer (1927):
Prandtl-Schlichting (1932):
Schoenherr (1932):
Schultz-Grunov (1940):
Kempf-Karman (1951):
Lap-Troost (1952):
Landweber (1953):
Hughes (1954):
Wieghard (1955):
ITTC (1957):
Gadd (1967):
Granville (1977):
Date Turnock (1999):
References
- von Karman, Theodore (1934), Turbulence and Skin Friction, J. of the Aeronautical Sciences, Vol. 1, No 1, 1934, pp. 1-20.
- Lazauskas, Leo Victor (2005), "Hydrodynamics of Advanced High-Speed Sealift Vessels", Master Thesis, University of Adelaide, Australia (download).
- Schlichting, Hermann (1979), Boundary Layer Theory, ISBN 0-07-055334-3, 7th Edition.
To do
Someone should add more data about total skin friction approximations, Prandtl-Schlichting skin-friction formula, and the Karman-Schoenherr equation. Add proper reference for equations in [2]

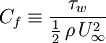
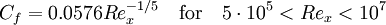
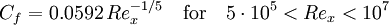
![C_f = [ 2 \, log_{10}(Re_x) - 0.65 ] ^{-2.3} \quad \mbox{for} \quad Re_x < 10^9](/W/images/math/c/a/4/ca4dc895c55260e9f9244eb0465141c8.png)
![C_f = 0.370 \, [ log_{10}(Re_x) ]^{-2.584}](/W/images/math/3/4/4/34492727370cbb6fa12a571f65a1388a.png)
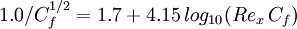
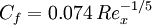
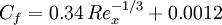
![C_f = 0.455 \, [ log_{10}(Re_x)]^{-2.58}](/W/images/math/5/4/6/5467f64b95b410d418b2e5257ccfa842.png)
![C_f = 0.0586 \, [ log_{10}(Re_x \, C_f )]^{-2}](/W/images/math/0/5/1/0517e14ad72f9e240a9d537681a68a5f.png)
![C_f = 0.427 \, [ log_{10}(Re_x) - 0.407]^{-2.64}](/W/images/math/b/d/0/bd032a44b9b3e0efb177d2095586e673.png)
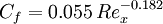
![C_f = 0.0648 \, [log_{10}(Re_x \, C_f^{0.5})-0.9526]^{-2}](/W/images/math/a/0/6/a06720ea4112676a8dfddf461267897c.png)
![C_f = 0.0816 \, [log_{10}(Re_x) - 1.703]^{-2}](/W/images/math/e/3/2/e3275545f39f2589f820703fbf0e68c5.png)
![C_f = 0.067 \, [log_{10}(Re_x) - 2 ] ^{-2}](/W/images/math/b/a/5/ba51e1668f07b0b204e2661190ccab3b.png)
![C_f = 0.52 \, [log_{10}(Re_x)] ^{-2.685}](/W/images/math/4/1/d/41d1dfc26b81ccb5141b86a44dc0e35e.png)
![C_f = 0.075 \, [log_{10}(Re_x) - 2 ] ^{-2}](/W/images/math/2/8/1/281d43a24f91a71bc89512dfd0e1e13c.png)
![C_f = 0.0113 \, [log_{10}(Re_x) - 3.7 ] ^{-1.15}](/W/images/math/9/7/f/97f180fb245f42f56db823a0433fe82a.png)
![C_f = 0.0776 \, [log_{10}(Re_x) - 1.88 ] ^{-2} + 60 \, Re_x^{-1}](/W/images/math/f/8/5/f858769b3aa5a365c535e5bf15745491.png)
![C_f = [4.06 \, log_{10}(Re_x \, C_f) - 0.729]^{-2}](/W/images/math/d/c/3/dc3b85bc6b0d869a9a558363fd876afb.png)