Stone's method
From CFD-Wiki
| Line 2: | Line 2: | ||
We have seen that '''LU''' decomposition is an excellent general purpose linear equation solver. The biggest disadvantage of these type of solver is they fail to take advantage of coefficient matrix. In preconditioned iterative methods, if the preconditioner matrix '''M''' is a good approximation of coefficient matrix '''A''' then the convergence is faster. This brings us to idea of using approximate factorization '''LU''' of '''A''' as the iteration matrix '''M'''. | We have seen that '''LU''' decomposition is an excellent general purpose linear equation solver. The biggest disadvantage of these type of solver is they fail to take advantage of coefficient matrix. In preconditioned iterative methods, if the preconditioner matrix '''M''' is a good approximation of coefficient matrix '''A''' then the convergence is faster. This brings us to idea of using approximate factorization '''LU''' of '''A''' as the iteration matrix '''M'''. | ||
A version of incomplete lower-upper decomposition method was proposed by '''Stone''' (1968). This method is also called the '''strongly implicit procedure''' or '''SIP'''. This method is designed for equation system arising from discretisation of partial differential equations. This method does not apply to generic system of equations. | A version of incomplete lower-upper decomposition method was proposed by '''Stone''' (1968). This method is also called the '''strongly implicit procedure''' or '''SIP'''. This method is designed for equation system arising from discretisation of partial differential equations. This method does not apply to generic system of equations. | ||
| + | |||
| + | ==Algorithm== | ||
| + | : '''A'''x = b <br> | ||
| + | : calculate Incomplete '''LU''' factorization of matrix '''A''' <br> | ||
| + | :: '''A'''x = ('''M'''-'''N''')x = ('''LU'''-'''N''')x = b <br> | ||
| + | :: '''M'''x<sup>(k+1)</sup> = '''N'''x<sup>(k)</sup>+b , with ||'''M'''|| >> ||'''N'''|| <br> | ||
| + | :: '''M'''x<sup>(k+1)</sup> = '''LU'''x<sup>(k+1)</sup> = c<sup>(k)</sup> <br> | ||
| + | :: '''LU'''x<sup>(k)</sup> = '''L'''('''U'''x<sup>(k+1)</sup>) = '''L'''y<sup>(k)</sup> = c<sup>(k)</sup> <br> | ||
| + | :: <br> | ||
| + | : set a guess | ||
| + | :: k = 0, x<sup>(k)</sup> <br> | ||
| + | :: r<sup>(k)</sup>=b - '''A'''x<sup>(k)</sup> <br> | ||
| + | : while ( ||r<sup>(k)</sup>||<sub>2</sub> <math> \ge \varepsilon </math>) do <br> | ||
| + | :: evaluate new right hand side | ||
| + | ::: c<sup>(k)</sup> = '''N'''x<sup>(k)</sup> + b <br> | ||
| + | :: solve '''L'''y<sup>(k)</sup> = c<sup>(k)</sup> by forward substitution <br> | ||
| + | ::: y<sup>(k)</sup> = '''L'''<sup>-1</sup>c<sup>(k)</sup> <br> | ||
| + | :: solve '''U'''x<sup>(k+1)</sup> = y<sup>(k)</sup> by back substitution <br> | ||
| + | ::: x<sup>(k+1)</sup> = '''U'''<sup>-1</sup>y<sup>(k)</sup> <br> | ||
| + | : end while | ||
| + | |||
| + | ---- | ||
Revision as of 06:15, 27 September 2005
Basic Concept
We have seen that LU decomposition is an excellent general purpose linear equation solver. The biggest disadvantage of these type of solver is they fail to take advantage of coefficient matrix. In preconditioned iterative methods, if the preconditioner matrix M is a good approximation of coefficient matrix A then the convergence is faster. This brings us to idea of using approximate factorization LU of A as the iteration matrix M. A version of incomplete lower-upper decomposition method was proposed by Stone (1968). This method is also called the strongly implicit procedure or SIP. This method is designed for equation system arising from discretisation of partial differential equations. This method does not apply to generic system of equations.
Algorithm
- Ax = b
- calculate Incomplete LU factorization of matrix A
- Ax = (M-N)x = (LU-N)x = b
- Mx(k+1) = Nx(k)+b , with ||M|| >> ||N||
- Mx(k+1) = LUx(k+1) = c(k)
- LUx(k) = L(Ux(k+1)) = Ly(k) = c(k)
-
- Ax = (M-N)x = (LU-N)x = b
- set a guess
- k = 0, x(k)
- r(k)=b - Ax(k)
- k = 0, x(k)
- while ( ||r(k)||2
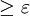 ) do
) do
- evaluate new right hand side
- c(k) = Nx(k) + b
- c(k) = Nx(k) + b
- solve Ly(k) = c(k) by forward substitution
- y(k) = L-1c(k)
- y(k) = L-1c(k)
- solve Ux(k+1) = y(k) by back substitution
- x(k+1) = U-1y(k)
- x(k+1) = U-1y(k)
- evaluate new right hand side
- end while
