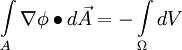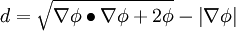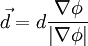Transport equation based wall distance calculation
From CFD-Wiki
Wall-distance variable
Wall distance are required for the implementation of various turbulence models.
The approaximate values of wall distance could be obtained by solving a transport equation for a variable called wall-distance variable or 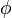 .
.
The transport equation for the wall distance variable could be written as:
with the boundary conditions of Dirichlet at the walls as 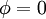 and Neumann at other boundaries as
and Neumann at other boundaries as 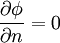
This transport equation could be solved with any of the approaches similar to that of Poisson's equation.
Wall distance calculation
Wall distance from the solution of this transport equation could be easily obtained as:
Where as the wall distance vector could be written as: