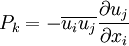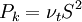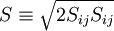Zeta-f model
From CFD-Wiki
(Difference between revisions)
Mirzapopovac (Talk | contribs) (→The turbulent viscosity <math>\nu_t</math>) |
Mirzapopovac (Talk | contribs) (→The turbulent kinetic energy <math>k</math>) |
||
| Line 6: | Line 6: | ||
<math>\nu_t = C_\mu \, \zeta \, k \, T</math> | <math>\nu_t = C_\mu \, \zeta \, k \, T</math> | ||
| - | == | + | == Turbulent kinetic energy <math>k</math> == |
<math>\frac{\partial k}{\partial t} + U_j \frac{\partial k}{\partial x_j} = P_k - \varepsilon + \frac{\partial}{\partial x_j} \left[ \left( \nu + \frac{\nu_t}{\sigma_{k}} \right) \frac{\partial k}{\partial x_j} \right]</math> | <math>\frac{\partial k}{\partial t} + U_j \frac{\partial k}{\partial x_j} = P_k - \varepsilon + \frac{\partial}{\partial x_j} \left[ \left( \nu + \frac{\nu_t}{\sigma_{k}} \right) \frac{\partial k}{\partial x_j} \right]</math> | ||
| - | |||
== The turbulent kinetic energy dissipation rate <math>\varepsilon</math> == | == The turbulent kinetic energy dissipation rate <math>\varepsilon</math> == | ||
Revision as of 12:26, 22 January 2007
The zeta-f model is a robust modification of the elliptic relaxation model. The set of equations, for the incompressible Newtonian fluid, constituting the  model is given below.
model is given below.
Turbulent viscosity 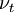
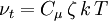
Turbulent kinetic energy 
![\frac{\partial k}{\partial t} + U_j \frac{\partial k}{\partial x_j} = P_k - \varepsilon + \frac{\partial}{\partial x_j} \left[ \left( \nu + \frac{\nu_t}{\sigma_{k}} \right) \frac{\partial k}{\partial x_j} \right]](/W/images/math/4/e/a/4eac951b79fdf4d26cac2b6cca1540bd.png)
The turbulent kinetic energy dissipation rate 
![\frac{\partial \varepsilon}{\partial t} + U_j \frac{\partial \varepsilon}{\partial x_j} = \frac{C_{\varepsilon 1} P_k - C_{\varepsilon 2} \varepsilon}{T} + \frac{\partial}{\partial x_j} \left[ \left( \nu + \frac{\nu_t}{\sigma_{\varepsilon}} \right) \frac{\partial \varepsilon}{\partial x_j} \right]](/W/images/math/5/b/e/5be411c44d64810a0a4d341ada81137c.png)
The normalized fluctuating velocity normal to the streamlines 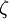
![\frac{\partial \zeta}{\partial t} + U_j \frac{\partial \zeta}{\partial x_j} = f - \frac{\zeta}{k} P_k + \frac{\partial}{\partial x_j} \left[ \left( \nu + \frac{\nu_t}{\sigma_{\zeta}} \right) \frac{\partial \zeta}{\partial x_j} \right]](/W/images/math/1/4/3/143979f772a60676f05d24a868fa7f47.png)
The elliptic relaxation function 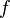
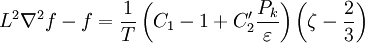
The production of the turbulent kinetic energy 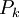
The modulus of the mean rate-of-strain tensor 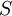
The turbulence time scale 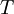
![T = max \left[ min \left( \frac{k}{\varepsilon},\, \frac{0.6}{\sqrt{6} C_{\mu} |S|\zeta} \right), C_T \left( \frac{\nu^3}{\varepsilon} \right)^{1/2} \right]](/W/images/math/6/1/7/617b18437b40d1988d1ca62041a1bca0.png)
The turbulence length scale 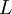
![L = C_L \, max \left[ min \left( \frac{k^{3/2}}{\varepsilon}, \,
\frac{k^{1/2}}{\sqrt{6} C_{\mu} |S| \zeta} \right), C_{\eta}
\left( \frac{\nu^3}{\varepsilon} \right)^{1/4} \right]](/W/images/math/7/0/7/70730f002515f1c28758512281d69cd2.png)
The coefficients
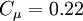 ,
, 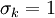 ,
, 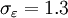 ,
, 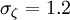 ,
, 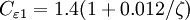 ,
, 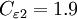 ,
, 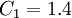 ,
, 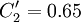 ,
, 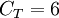 ,
, 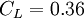 and
and 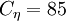 .
.
References
- Popovac, M., Hanjalic, K. Compound Wall Treatment for RANS Computation of Complex Turbulent Flows and Heat Transfer, Flow, Turbulence and Combustion, DOI 10.1007/s10494-006-9067-x, 2007.
- Hanjalic, K., Popovac, M., Hadziabdic, M. A robust near-wall elliptic-relaxation eddy-viscosity turbulence model for CFD, Int. J. Heat Fluid Flow, 25, 1047–1051, 2004.