
 |
Relation between Wall shear stress and rate of strain tensor
|
Thank you for your reply, My goal is to get the expression of the wall shear stress from viscous stress tensor (details below), but I am stuck in the final steps. I wonder why the terms:
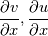 , and , and 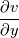 vanish at the wall? vanish at the wall?Here is what I've done so far: Let's consider a 2D incompressible laminar flow, of a newtonian fluid; The viscous stress tensor is given by:  Where 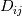 is the rate of strain and is given by: is the rate of strain and is given by: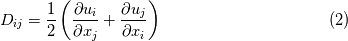 The viscous stress vector at a surface with a normal 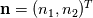 is given by: is given by: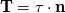 Or: 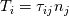 In other words: 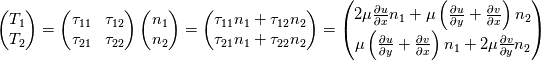 Now, I am stuck, How to proceed further to get the wall shear stress expression, could you please help me? |
Quote:
Yes it depend on all the strain components and it is quite difficult to derive than to calculate a generic formula. The formula you mentioned is for 2D flow with wall parallel to y-axis. It indicates derivative of resultant tangential velocity normal to the wall. |
Quote:
Once you got force components take only the tangential force which acts on the wall. Derivation of this is difficult for generic wall orientation in 3D. For 2D it is Fx*ny - Fy*nx. Also apply u.n=0 (wall normal velocity is zero). |
For incompressible 2d flows you have the divergence-free constraint that, written on the wall reduces to dv/dy=0
|
|
|
Quote:
But that's not necessarily true for a general curved wall (e.g airfoil). |
Quote:
it is still true if you write the expression in curvilinear coordinates, i.e., normal and tangential directions |
Quote:
since we chose to write the equations in curvilinear coordinates, we have: 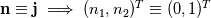 hence: 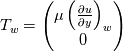 And since the wall shear stress is the tangential component of the viscous stress vector at the wall, we get: 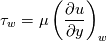 |
| All times are GMT -4. The time now is 20:01. |