 |
|
|
[Sponsors] | |||||
LES Filtering: how are the small and large scales equations solved? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
ATM
Join Date: May 2009
Location: United States
Posts: 104
Rep Power: 16  |
Hi,
I have read many journals , which advocate implicit and explicit filtering.(Though implicit is almost always used). I'm yet to clearly understand how exactly the process of filtering works in the LES algorithm.This is my understanding of implicit filtering, Please correct it if I am wrong : 1) The LES governing equations containing the "filtered" terms and the subrid scale tensor 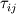 are solved using some numerical scheme - e.g. SIMPLE. are solved using some numerical scheme - e.g. SIMPLE.2) The terms in the continuity and momentum equations - the velocity and pressure etc are solved for exactly the way normal Navier Stokes eqns are solved.i.e. Poisson;s eqn to solve for pressure, guessing the initial velocity field etc. 3) The subgrid tensor term is modeled using Smagorinsky or any other empirical model for EVERY cell in the mesh, where the LES equations are applied.i.e. the 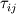 term is modeled in the equation for all mesh sizes, even when larger scales are being solved for. term is modeled in the equation for all mesh sizes, even when larger scales are being solved for.--------------- So basically, is it that the LES governing equations are solved just like the traditional NS equations, but the difference being that an extra subgrid tensor has to be included in the equation every time, to include the effect of the smaller scales? So in essence, we can thus use a coarser mesh so that the LES eqns resolve the larger scales, and the subgrid term in the eqn, models the smaller scales, which are not able to be resolved due to the mesh not being fine enough? I was just wondering where the actual "filtering" process takes place in the code....is it just a mathematical definition which is used to derive the LES eqns?Coz' all I can see here are a modified form of the NS eqns and a subgrid term which is modeled. Hence, I guess the solution algorithm for a LES code would be almost same as the traditional incompressible NS solver, except for the fact that I would have to compute 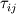 , and include it in the main NS eqns. , and include it in the main NS eqns.As I said, kindly correct me wherever I am wrong here. I have gone through almost all the older threads relating to this in the forum, but I couldn't get this cleared.I have to start writing a LES code myself, and hence i feel I have to be very strong in these concepts before I embark on it. I know this has been a long question., and I would really appreciate anyone offering their help . Thanks in advance. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
The question that you have is fundamental in LES, since many confusion still exists....
- implicit filtering: The governing filtered equations in LES are never acted upon an explicit filtering in the code (apart from the use of SGS dynamic procedure). Therefore, the filtering is provided implicitly by two causes, the computational grid (induces a cut-off at Nyquist frequency) and the discretization used in the code (that can change the shape of the implicit transfer function). The SGS model is some way imply the type of filtering. If you see the mathematical LES equation, you could confuse them for URANS equations! The difference is in the SGS term and in the fact that in LES you generally use high order accurate discretizations. The type of filtering (sharp cut-off, top-hat, gaussian, ecc.) is due to the discretization. - Explicit filtering: you explicitly apply a filtering procedure on the non-linear terms. This way you want to explicitly control the shape of the filtering (that you really choose) and eliminate numerical errors at high resolved wavenumbers Much more details about this issue were described in: http://www.sciencedirect.com/science...21999111000933 Good work |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
ATM
Join Date: May 2009
Location: United States
Posts: 104
Rep Power: 16  |
Thank you very much FMDenaro!!
I am much clear now.So Basically, I just solve it like the normal NS eqns, but with the subgrid term and a higher order discretization... As for explicit filtering, I come across various discrete explicit filter equations in journals, esp. the 3 - point filter like this, 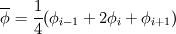 Now my question is: Is the way it works that the implicit LES equations are solved first, at every cell, and then the explicit discrete filter is applied to the implicit LES solution to obtain the "explicit filtered field"? Is it just like an averaging operation to obtain the explicit filtered value at a cell by taking weighted averages of the values in the cells in the neighboring region? So I assume that, when discrete explicit Gaussian filters are used, the "weights" are decided by the cutoff length of the filter and the mesh spacing at every cell. i.e. the ratio 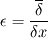 (where (where 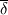 is the cutoff length and is the cutoff length and 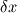 is the mesh spacing) is used in the definition of the Gaussian discrete explicit filter. is the mesh spacing) is used in the definition of the Gaussian discrete explicit filter.This way, wont it make the explicit LES a two step process? - increasing computational time and cost? What is the biggest benefit of this explicit filtering, except for the fact that the LES solution is no longer dependent on the grid spacing? I dont understand the idea as to why "averaging" an already implicit filtered field would improve accuracy.It would be nice if you could shed some light on this. Once again, I thank you for your time !! P.S. : I am going through your paper, and I must say that it clears a lot of things I had questions about.Its really good. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
I'm happy to be of some help.
About explicit filtering, I can resume the two general way you can find in literature (if you see the references in my paper you will find 3 - 4 papers discussing explicit filtering) - Apply an explicit filtering to the implicit LES solution at each time-step. It was demonstrated by some authors (e.g. Lund) that this is not consistent, you will get a [V_bar]_bar solution that does not satisfy a filtered equation. - Apply an explicit filtering to the non-linear flux, that is [U_bar* U_bar]_bar. This is more congruent to the governing filtered equation, it controls the numerical errors and generally you need a filter lenght from 2 to 4 times the mesh size. Of course you will get a reduced resolution. Explicit filtering requires some more computational effort. It is still controversial if use it or not ... |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
ATM
Join Date: May 2009
Location: United States
Posts: 104
Rep Power: 16  |
That makes things more clear...
Thank you very much for your help! |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Just to add a comment, at best of my knowledge explicit filtering is only an acadamic issue, no commercial LES code (FLuent, TransAT, etc) or open-source (OpenFOAM, Code_Saturne) use that, the filter is always implicitly defined by the discretization.
That makes very often confusing to distinguish in the manuals the LES from URAN equations, they are written formally in the same way.. |
|
|
|

|
|
|
|
|
#7 |
|
Member
Francesco Capuano
Join Date: May 2010
Posts: 81
Rep Power: 15  |
I am very interested in filtering issues for LES. As a relatively new researcher in the field, I really agree with Filippo when he says that there is much confusion about filtering; this is probably due to the fact that there is not a unique and accepted classification regarding implicit / explicit filtering techniques and so on. I still don't understand why many authors, when using LES, do not even mention which type of filtering has been used, or do not link the grid resolution to the Nyquist cut-off wavenumber and the dissipation scales.
Furthermore, there is often confusion between the mathematical model used to derive the LES equations (i.e. the convolution filter model, at foremost) and the practical LES, in which grid and discretization filters are always present. Even in a very good book like that by Pope such concepts are pretty misleading, in my opinion. OpenFOAM offers a number of dynamic models, and therefore some discrete filters are already implemented; one interesting thing which I would like to try is to exploit those built-in routines to create a solver for explicitly filtered LES. I wonder if someone has already done it... |
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
you are right and it is very difficult for a newcomer in LES to focus on filtering issue... Many often the authors say simply "top-hat" when they use second order FD/FV and spectral cut-off when using spectral methods... but the real shape of the transfer function can be affected by many factors... For years I tried to understand among several papers the correct way to address such an issue... I tried in my paper on JCP (cited above) to clarify what I now understand about filtering, I hope that reading it you can find some useful topic  But I know that many things remain to be addressed ... |
||
|
|

|
||
|
|
|
#9 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
I suggest starting with a very simple test: use a velocity field coming from a well established simulation (with known spectra) and apply the discrete filters implemented in OF. Then analyze the resulting spectra in the directions to understand what the filter real does... This is the first thing to understand |
||
|
|

|
||
|
|
|
#10 | ||
|
Member
Francesco Capuano
Join Date: May 2010
Posts: 81
Rep Power: 15  |
Quote:
 Your paper was very usfeul to clarify many fundamental concepts. My feeling (but of course it's a newcomer's feeling Your paper was very usfeul to clarify many fundamental concepts. My feeling (but of course it's a newcomer's feeling  ) is that LES community should put more effort in clarifying filtering issues; a unified and "conventional" nomenclature would be a good start too... ) is that LES community should put more effort in clarifying filtering issues; a unified and "conventional" nomenclature would be a good start too...Quote:
|
|||
|
|

|
|||
|
|
|
#11 | |
|
Senior Member
ATM
Join Date: May 2009
Location: United States
Posts: 104
Rep Power: 16  |
Quote:
I completely agree on this. The practical form of LES filtered equations and the theoretical form (convolution filter mathematical derivations) etc are not related to clearly by many authors. I'm glad Prof. Denaro cleared the confusion here. I have a question - when we apply the filtered equations, we solve for the subgrid stresses in the equation at every grid/cell, don't we? So this means that we *assume* there are scales smaller than the subgrid scale in every region (every gridpoint) of the flow. What if this is not the case in some regions? Won't the code give unphysical results in these regions? Is there a way in which the subgrid stresses can be evaluated in only in some regions of the grid, while we don't in others? Thanks for your time. |
||
|
|

|
||
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
that happens automatically in a well-built SGS model for LES.... for example, the dynamic Smagorinsky procedure leads to a vanishing eddy viscosity if the flow is laminar. You can see many papers where the eddy visosity profile is reported, for example in channel flow, and goes to zero in the viscous sub-layer. This is a great difference with RANS formulation where the model acts along all scales, affecting also laminar region. |
||
|
|

|
||
|
|
|
#13 | |
|
Senior Member
ATM
Join Date: May 2009
Location: United States
Posts: 104
Rep Power: 16  |
Quote:
Thanks again. I was actually thinking of implementing the ordinary Smagorinsky model with a Cs =0.1 ( which the Fluent documentation says is a good guess to avoid excessive diffusion in large scale structures). In dynamic Smagorinsky, I know that we have to apply a test filter with a width twice that of the grid filter and the difference in the resolved scales between the two filters would aid in computation of the constant C_s. Now, Doesn't this actually look like explicit filtering? If my understanding is correct, we have to resolve the grid filter , and the apply some sort of discrete explicit filter (like the 3 point filter in my earlier post) to account for the test filter, and use the resolved fields obtained from both the filters, to calculate the smagorinsky constant using the Germano identity. is this correct? or is method of applying the test filter different ? Thanks. |
||
|
|

|
||
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
The explicit filtering in LES involves the application of a filter on the convective flux in the momentum equation whilst (as you stated) the dynamic procedure is based on the application of a test-filter on all the terms of the equation, and the Germano identity is derived for the SGS tensors. Both procedures require an algorithm for doing an explicit filtering. What kind of discrete filtering works the best is a further complex issue.... |
||
|
|

|
||
|
|
|
#15 | |
|
Senior Member
ATM
Join Date: May 2009
Location: United States
Posts: 104
Rep Power: 16  |
Quote:
Its more clear now.....I guess I will implement the ordinary Smagorinsky model as of now, since this is going to be my first LES code, and then move on to the dynamic model if required. Thank you for you help all along, Prof Denaro! |
||
|
|

|
||
|
|
|
#16 | |
|
Member
Francesco Capuano
Join Date: May 2010
Posts: 81
Rep Power: 15  |
Quote:
Now, my doubt is: which part of a (let's say dynamic) SGS model is responsible for this? Is it the dynamic calculation of the constant? I guess the standard Smagorinsky is not capable of doing that, as the constant is fixed and is calculated assuming, a priori, a certain position of the filter width along the spectrum, is that right? |
||
|
|

|
||
|
|
|
#17 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
Have a good work |
||
|
|

|
||
|
|
|
#18 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
well, you can observe that the filtered velocity can be written in the Fourier space as u_bar(k)=G(k)*u(k). When apply a test filtering (its transfer function I call T), you have [u_bar]_test(k)=T(k)*G(k)*u(k). In laminar flows you have only very low wavenumber components where T and G become practically =1. So, the test-filtered velocity is equal to the grid-filtered velocity and the SGS term will vanish ... see the Germano identity and modelling. For the static Smagorinsky model, when the flow has some direction in which is not homogeneous (for example in channel flow), it is advised to use the Van Driest damping function that depends on the local position. Note that convergence of an LES solution towards DNS for refined grids is true only if you do not use explicit filtering. |
||
|
|

|
||
|
|
|
#19 |
|
Member
Francesco Capuano
Join Date: May 2010
Posts: 81
Rep Power: 15  |
Ok, clear, thank you.
I was also trying to better understand the relationship between the filter width and the model constant. Considering a static Smagorinsky, I guess we cannot use the same constant if the filter width is in the dissipation range (i.e. very fine grid) or if it is in the inertial subrange. For example, if I remember well, the Lilly's constant for the Smagorinsky model is calculated assuming the filter width in the inertial sub-range. However, this is maybe unuseful, because for small filter widths the viscous stress should be much higher than the residual stress. |
|
|
|

|
|
|
|
|
#20 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
Delta is someway related to the computational grid measure, therefore for non uniform grids also Delta=Delta(x). Therefore (Cs*Delta)^2 depends on the position. You can see the great advantage of the dynamic procedure that allows us to compute locally all the term (Cs*Delta)^2. The static Smagorinsky requires some ad hoc adjustement. As I wrote before, the example of the channel is good. Assume a grid very refined near the wall, so that you have some points before y+=1. This way practically the filter size is at DNS resolution in the boundary layer. The static Smagorinsky viscosity must be damped by using the Van Driest dumping. Conversely, the dynamic Smagorinsky works automatically! 
|
||
|
|

|
||
 |
| Tags |
| filter, les, navier stokes equation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Y+ value for Large Eddy Simulation | yannossss | Main CFD Forum | 15 | March 21, 2017 23:41 |
| Filtering in Large Eddy Simulation | maybee | Main CFD Forum | 7 | May 19, 2014 16:21 |
| [ICEM] Large and small cylinder with inner wall | Far | ANSYS Meshing & Geometry | 5 | March 27, 2012 07:56 |
| Simulating small features on large models | siw | CFX | 1 | February 16, 2012 17:10 |
| what happens if y+ is too large or too small | Bo Jensen | Siemens | 12 | February 19, 2003 23:31 |