 |
|
|
[Sponsors] | |||||
Euler Equations, Sod shock tube & conservation |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Jun 2014
Posts: 1
Rep Power: 0  |
Is momemtum conserved?
I am considering the Euler equations in conservative form and solving the Sod shock tube problem I have written a Godunov finite volume type solver. It solves for density ρ, momentum ρu, and total energy E; therefore, I would expect all of these quantities to be conserved wrt time. Density and total energy are indeed conserved, however, momentum is not. The Euler equations are given by 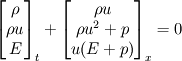 where pressure is related to the conserved quantities by 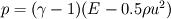 The Sod shock problem splits the domain into two regions separated by a density and pressure discontinuity with initial velocity zero. That is, 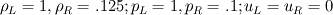 These initial conditions imply that ρu=0, therefore, momentum should be zero throughout the simulation. These initial conditions imply that ρu=0, therefore, momentum should be zero throughout the simulation.The solution profiles are well known and can be found here or here. We see that ρ >0 and u > 0, therefore, there is no way for momentum ρu = 0 (which it should be from the intial conditions). As a result, I do not even see why it is reasonable to expect that momentum would be conserved. A paper by Sod himself which surveys some methods for solution, on page 20, list a table which shows momentum is not conserved, but no reason why. I generally do not work in this area, so maybe I am missing something basic. Can anyone shed some light on this? Thanks! |
|
|
|

|
|
|
|
|
#2 |
|
Member
Join Date: Jul 2013
Posts: 55
Rep Power: 12  |
In the way I see Sod shock tube, there is a seal between the two region (left and right). Since the pressure on both side are not equal, there is a net force applied by the fluid on the seal. Using Newton's 3rd law, the seal also applies a net force on the fluid. Momentum is only conserved if no external forces are applied on the system, which is not the case here.
As soon as the seal is removed from the system (or broken) there is a discontinuity in pressure and density. The very first fluid element, adjacent to this pressure discontinuity, moves at a very high velocity, with all the momentum of the domain. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Shock tube simulation in Fluent | Vinoo_P | FLUENT | 28 | September 6, 2018 00:21 |
| Analytic solution for 2D steady Euler equations | jojo81 | Main CFD Forum | 0 | October 15, 2012 12:05 |
| rhoCentralFoam not reflecting shock in Shock Tube? | Astaria | OpenFOAM Running, Solving & CFD | 5 | March 4, 2012 03:07 |
| Euler equations & expansion shocks | technophobe | Main CFD Forum | 5 | April 28, 2009 15:11 |
| Euler equations? | Jan Ramboer | Main CFD Forum | 2 | August 19, 1999 01:58 |