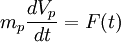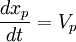Two phase flow
From CFD-Wiki
(→Lagrangian dispersed two-phase flow modelling) |
(→Lagrangian dispersed two-phase flow modelling) |
||
| Line 28: | Line 28: | ||
</math> | </math> | ||
| - | The instantaneous fluid velocity | + | The instantaneous fluid velocity <math> {u_i} </math> is decomposed into a mean part which is known (from turbulence model prediction) and a fluctuating part <math> {u_i}^{'} </math>. |
In 2D description, we have to determine a vector of correlated random variables: | In 2D description, we have to determine a vector of correlated random variables: | ||
U’= (ui'(0), uj’ (0)... ui’ (nt), uj’ (nt) ...) | U’= (ui'(0), uj’ (0)... ui’ (nt), uj’ (nt) ...) | ||
Revision as of 12:42, 24 September 2007
Contents |
Introduction
article in progress
Importance of two phase flow in industrial configurations
Two phase flow phenomena occur in various industrial application in all fluid mechanics application fiels. Aerospace, automotive, nuclear applications, etc. In all this domain, prediction of two phase behaviour is important. Prediction of liquid spray in an internal combustion engine should enable us to have a better control on combustion process and then to reduce pollutant emissions. Controlling water - steam equilibrium in a coller system enable to prevent from industrial accident, de-icing/anti-icing of aircraft on the ground etc. Any other examples can be quoted here.
Overview of the different available approach
Two main family can be distinguished to model two phase flow, depending of the two phase configuration approach. In case of dispersed configuration a lagrangian approach is suitable. Such an approach consists in following dropplets (or bubbles) during then movement. This is done by applying external force on the particle and solving acceleration, then velocity and finally position. On the other hand, two phase flow can be solve with an eulerien approach. As in all eulerian framework, this approach consists in considering inlet and outlet flux in a given volume. In such an eulerian approach, two family can be distinguished : Mixture model and Two fluids model, those two approach will be detailed in corresponding section bellow.
Lagrangian dispersed two-phase flow modelling
The main goal in Lagrangien approaches is to statiscally particle history in given flow fields. The starting point in Lagrangien approach is the fundamental law of dynamics:
Where 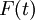 stands for the resulting force on the particle.
Resolution of these equations requires the knowledge of the instantaneous velocity of the fluid at particle position. The problem is thus to track fluid particles along the discrete particle trajectory.
A fluid particle instantaneously owns the velocity of the surrounding fluid and the simulation of its trajectory relies on a quite simple equation such as:
stands for the resulting force on the particle.
Resolution of these equations requires the knowledge of the instantaneous velocity of the fluid at particle position. The problem is thus to track fluid particles along the discrete particle trajectory.
A fluid particle instantaneously owns the velocity of the surrounding fluid and the simulation of its trajectory relies on a quite simple equation such as:
The instantaneous fluid velocity 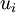 is decomposed into a mean part which is known (from turbulence model prediction) and a fluctuating part
is decomposed into a mean part which is known (from turbulence model prediction) and a fluctuating part 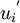 .
In 2D description, we have to determine a vector of correlated random variables:
U’= (ui'(0), uj’ (0)... ui’ (nt), uj’ (nt) ...)
where u’(nt) is the fluid fluctuating velocity at time nt.
U’ is determinate Starting from a vector Y(yi) of non correlated random numbers with a Gaussian distribution (<yi>=0 and<yiyj>=ij),
It is important to keep in mind that particle dispersion is roughly proportional to the turbulence time/length scales.
.
In 2D description, we have to determine a vector of correlated random variables:
U’= (ui'(0), uj’ (0)... ui’ (nt), uj’ (nt) ...)
where u’(nt) is the fluid fluctuating velocity at time nt.
U’ is determinate Starting from a vector Y(yi) of non correlated random numbers with a Gaussian distribution (<yi>=0 and<yiyj>=ij),
It is important to keep in mind that particle dispersion is roughly proportional to the turbulence time/length scales.
Mixture model for two phase flow
Basics of the mixture model
MAC approach
VOF method
Eulerian Two fluids approach
Basics of the two fluids approach
Interfacial exchange closures
Turbulence modelling in such a context
Conclusion
References
- Gosman A. D., Ionnides I. E. (1981), "Aspects of computer simulation of liqued fuelled combustors", AIAA aerospace sciences meeting, paper 81-0323, St.louis,MO.
- Boughattas N., Gazzah M. H., Said R. (2006), "Effects of a co-flow on particles or droplets dispersion and on droplets vaporization in turbulent air flow", ICAMEM2006, Hammamet, Tunisia.