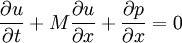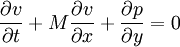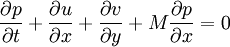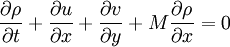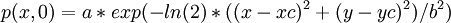2-D linearised Euler equation
From CFD-Wiki
(Difference between revisions)
| Line 16: | Line 16: | ||
== Results == | == Results == | ||
Pressure | Pressure | ||
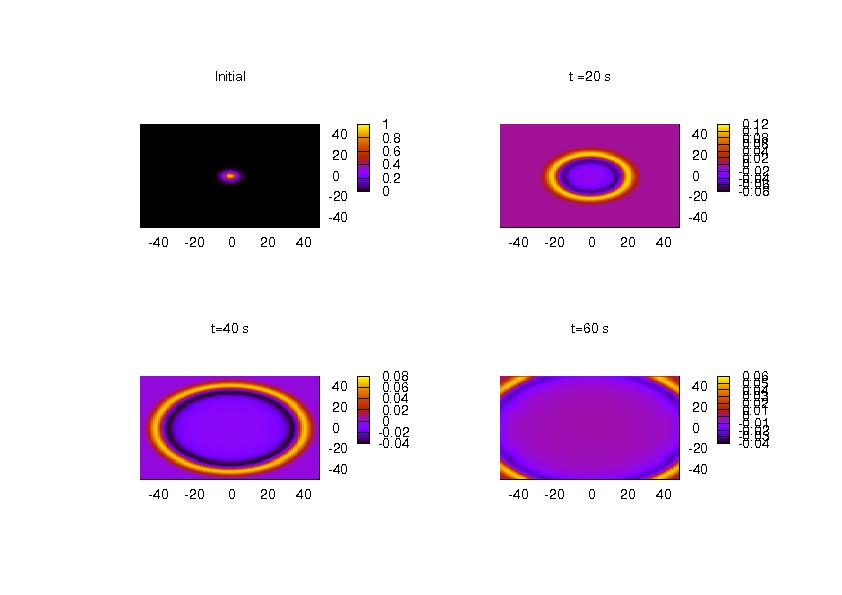
| - | No mean flow | + | :No mean flow |
[[Image:Nomeanflow.jpg]] | [[Image:Nomeanflow.jpg]] | ||
| + | :Mean Flow to left at U=0.5 (c assumed to be 1 m/s) | ||
| + | [[Image:Meanflow.jpg]] | ||
Uniform Mean flow to the left at U=0.5 (speed of sound assumed to be 1) | Uniform Mean flow to the left at U=0.5 (speed of sound assumed to be 1) | ||
Revision as of 07:40, 12 November 2005
Contents |
Problem Definition
where M is the mach number , speed of sound is assumed to be 1, all the variabled refer to acoustic perturbations over the mean flow.
Domain
[-50,50]*[-50,50]
Initial Condition
Boundary Condition
Characteristic Boundary Condition
Numerical Method
4th Order Compact scheme in space 4th order low storage RK in time
Results
Pressure
- No mean flow
- Mean Flow to left at U=0.5 (c assumed to be 1 m/s)
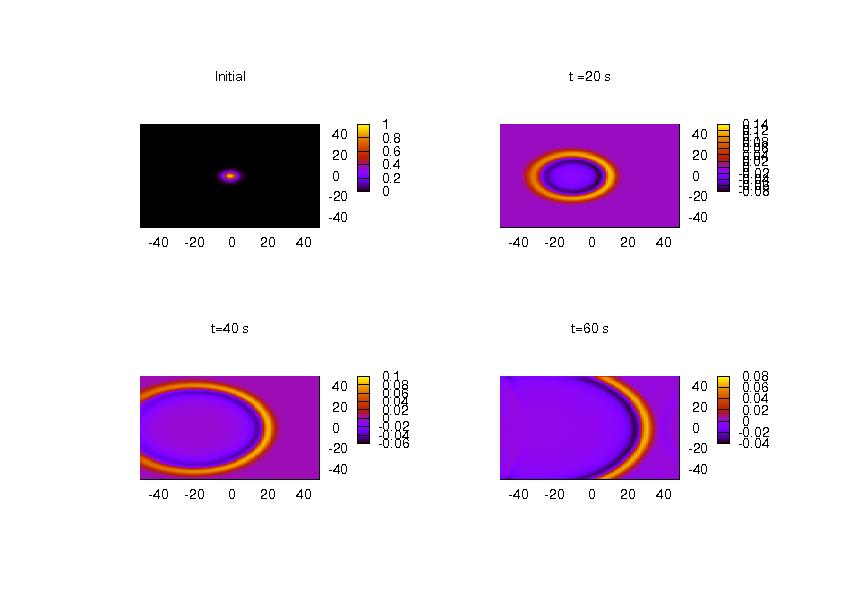 Uniform Mean flow to the left at U=0.5 (speed of sound assumed to be 1)
Uniform Mean flow to the left at U=0.5 (speed of sound assumed to be 1)
Reference
- Williamson, Williamson (1980), "Low Storage Runge-Kutta Schemes", Journal of Computational Physics, Vol.35, pp.48–56.
- Lele, Lele, S. K. (1992), "Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics", Journal of Computational Physics, Vol. 103, pp 16–42.