Cebeci-Smith model
From CFD-Wiki
(Copied from B-L model, still pretty rough) |
m (Reverted edits by RicgeTcnac (Talk) to last version by Merrifj) |
||
| (8 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | {{Turbulence modeling}} | |
| - | + | The Cebeci-Smith [[#References|[Smith and Cebeci (1967)]]] is a two-layer algebraic 0-equation model which gives the eddy viscosity, <math>\mu_t</math>, as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace applications. Like the [[Baldwin-Lomax model]], this model is not suitable for cases with large separated regions and significant curvature/rotation effects. Unlike the [[Baldwin-Lomax model]], this model requires the determination of of a boundary layer edge. | |
| - | The Cebeci-Smith [[#References|[Cebeci | + | |
== Equations == | == Equations == | ||
| - | <table width=" | + | <table width="70%"><tr><td> |
:<math> | :<math> | ||
\mu_t = | \mu_t = | ||
\begin{cases} | \begin{cases} | ||
{\mu_t}_{inner} & \mbox{if } y \le y_{crossover} \\ | {\mu_t}_{inner} & \mbox{if } y \le y_{crossover} \\ | ||
| - | {\mu_t}_{outer} & \mbox{if} y > y_{crossover} | + | {\mu_t}_{outer} & \mbox{if } y > y_{crossover} |
\end{cases} | \end{cases} | ||
</math></td><td width="5%">(1)</td></tr></table> | </math></td><td width="5%">(1)</td></tr></table> | ||
| Line 16: | Line 15: | ||
where <math>y_{crossover}</math> is the smallest distance from the surface where <math>{\mu_t}_{inner}</math> is equal to <math>{\mu_t}_{outer}</math>: | where <math>y_{crossover}</math> is the smallest distance from the surface where <math>{\mu_t}_{inner}</math> is equal to <math>{\mu_t}_{outer}</math>: | ||
| - | <table width=" | + | <table width="70%"><tr><td> |
:<math> | :<math> | ||
y_{crossover} = MIN(y) \ : \ {\mu_t}_{inner} = {\mu_t}_{outer} | y_{crossover} = MIN(y) \ : \ {\mu_t}_{inner} = {\mu_t}_{outer} | ||
</math></td><td width="5%">(2)</td></tr></table> | </math></td><td width="5%">(2)</td></tr></table> | ||
| - | The inner region is given | + | The inner region is given |
| - | <table width=" | + | <table width="70%"><tr><td> |
:<math> | :<math> | ||
| - | {\mu_t}_{inner} = \rho l^2 \left | + | {\mu_t}_{inner} = \rho l^2 \left[\left( |
| + | \frac{\partial U}{\partial y}\right)^2 + | ||
| + | \left(\frac{\partial V}{\partial x}\right)^2 | ||
| + | \right]^{1/2}, | ||
</math></td><td width="5%">(3)</td></tr></table> | </math></td><td width="5%">(3)</td></tr></table> | ||
where | where | ||
| - | <table width=" | + | <table width="70%"><tr><td> |
:<math> | :<math> | ||
l = \kappa y \left( 1 - e^{\frac{-y^+}{A^+}} \right) | l = \kappa y \left( 1 - e^{\frac{-y^+}{A^+}} \right) | ||
</math></td><td width="5%">(4)</td></tr></table> | </math></td><td width="5%">(4)</td></tr></table> | ||
| - | + | with the constant <math>\kappa = 0.4</math> and | |
| - | + | ||
| - | \kappa = 0.4 | + | |
| - | </math> | + | |
| - | <table width=" | + | <table width="70%"><tr><td> |
:<math> | :<math> | ||
| - | \left | + | A^+ = 26\left[1+y\frac{dP/dx}{\rho u_\tau^2}\right]^{-1/2}. |
</math></td><td width="5%">(5)</td></tr></table> | </math></td><td width="5%">(5)</td></tr></table> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
The outer region is given by: | The outer region is given by: | ||
| - | <table width=" | + | <table width="70%"><tr><td> |
:<math> | :<math> | ||
{\mu_t}_{outer} = \alpha \rho U_e \delta_v^* F_{KLEB}(y;\delta), | {\mu_t}_{outer} = \alpha \rho U_e \delta_v^* F_{KLEB}(y;\delta), | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(6)</td></tr></table> |
| - | where <math>\alpha=0.0168</math> | + | where <math>\alpha=0.0168</math> and <math>\delta_v^*</math> is the velocity thickness given by |
| - | <table width=" | + | <table width="70%"><tr><td> |
:<math> | :<math> | ||
| - | \delta_v^* = \int_0^\delta (1-U/U_e)dy | + | \delta_v^* = \int_0^\delta (1-U/U_e)dy. |
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(7)</td></tr></table> |
| - | + | <math>F_{KLEB}</math> is the Klebanoff intermittency function given by | |
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
| Line 74: | Line 64: | ||
F_{KLEB}(y;\delta) = \left[1 + 5.5 \left( \frac{y}{\delta} \right)^6 | F_{KLEB}(y;\delta) = \left[1 + 5.5 \left( \frac{y}{\delta} \right)^6 | ||
\right]^{-1} | \right]^{-1} | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(8)</td></tr></table> |
| - | + | ||
== Model variants == | == Model variants == | ||
| Line 88: | Line 77: | ||
== References == | == References == | ||
| - | * | + | * {{reference-paper|author=Smith, A.M.O. and Cebeci, T. |year=1967|title=Numerical solution of the turbulent boundary layer equations|rest=Douglas aircraft division report DAC 33735}} |
* {{reference-book|author=Wilcox, D.C. |year=1998|title=Turbulence Modeling for CFD|rest=ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc.}} | * {{reference-book|author=Wilcox, D.C. |year=1998|title=Turbulence Modeling for CFD|rest=ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc.}} | ||
| + | |||
| + | [[Category:Turbulence models]] | ||
| + | |||
| + | {{stub}} | ||
Latest revision as of 12:13, 18 December 2008
The Cebeci-Smith [Smith and Cebeci (1967)] is a two-layer algebraic 0-equation model which gives the eddy viscosity, 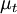 , as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace applications. Like the Baldwin-Lomax model, this model is not suitable for cases with large separated regions and significant curvature/rotation effects. Unlike the Baldwin-Lomax model, this model requires the determination of of a boundary layer edge.
, as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace applications. Like the Baldwin-Lomax model, this model is not suitable for cases with large separated regions and significant curvature/rotation effects. Unlike the Baldwin-Lomax model, this model requires the determination of of a boundary layer edge.
Contents |
Equations
|
| (1) |
where 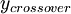 is the smallest distance from the surface where
is the smallest distance from the surface where 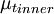 is equal to
is equal to 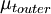 :
:
|
| (2) |
The inner region is given
|
| (3) |
where
|
| (4) |
with the constant 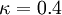 and
and
|
| (5) |
The outer region is given by:
|
| (6) |
where 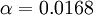 and
and 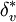 is the velocity thickness given by
is the velocity thickness given by
|
| (7) |
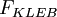 is the Klebanoff intermittency function given by
is the Klebanoff intermittency function given by
|
| (8) |
Model variants
Performance, applicability and limitations
Implementation issues
References
- Smith, A.M.O. and Cebeci, T. (1967), "Numerical solution of the turbulent boundary layer equations", Douglas aircraft division report DAC 33735.
- Wilcox, D.C. (1998), Turbulence Modeling for CFD, ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc..

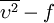 model
model
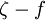 model
model
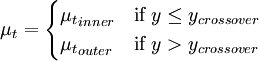
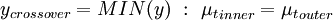
![{\mu_t}_{inner} = \rho l^2 \left[\left(
\frac{\partial U}{\partial y}\right)^2 +
\left(\frac{\partial V}{\partial x}\right)^2
\right]^{1/2},](/W/images/math/1/9/8/1980c3a67fd85d63d3e39f1d4784c606.png)
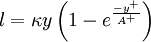
![A^+ = 26\left[1+y\frac{dP/dx}{\rho u_\tau^2}\right]^{-1/2}.](/W/images/math/1/9/8/19839d857afa6c50f418ac133d894115.png)
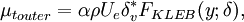
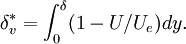
![F_{KLEB}(y;\delta) = \left[1 + 5.5 \left( \frac{y}{\delta} \right)^6
\right]^{-1}](/W/images/math/4/3/3/4331b74159c7e4947a91a3c15e2c8282.png)