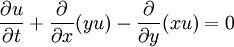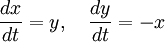Circular advection
From CFD-Wiki
The scalar advection equation
models advection along concentric circles. The characteristics are given by
and they are concentric circles about the origin going in clockwise direction. Any given initial condition is advected in circles without change of shape or magnitude. This is a good test case for assessing the numerical viscosity in a scheme.