Code: 3D Lid-driven cavity using pressure-free velocity form
From CFD-Wiki
| Line 43: | Line 43: | ||
</pre> | </pre> | ||
| - | === Diffusion matrix for pressure-free velocity method ('''DMat3D8W.m''')=== | + | ===[[PFV 3D diffusion matrix | 3D Diffusion matrix for pressure-free velocity method ('''DMat3D8W.m''')]]=== |
| - | === Convection matrix for pressure-free velocity method ('''CMat3D8W.m''')=== | + | ===[[PFV 3D convection matrix | 3D Convection matrix for pressure-free velocity method ('''CMat3D8W.m''')]]=== |
| + | |||
| + | ===[[PFV V8cW 3D linear FE | 3D linear divergence-free velocity element ('''V8cW.m''')]]=== | ||
| + | |||
| + | ===[[PFV V8xyzcW 3D linear FE derivatives | 3D first derivatives of linear velocity ('''V8xyzcW.m''')]]=== | ||
===[[PFV GMRES solver| GMRES solver with ILU preconditioning and Essential BC ('''ilu_gmres_with_EBC.m''')]]=== | ===[[PFV GMRES solver| GMRES solver with ILU preconditioning and Essential BC ('''ilu_gmres_with_EBC.m''')]]=== | ||
Revision as of 11:53, 20 July 2011
3D Lid-driven cavity using pressure-free velocity formulation
This sample code uses eight-node linear Hermite finite elements with simple iteration.
Theory
The incompressible Navier-Stokes equation is a differential algebraic equation, having the inconvenient feature that there is no explicit mechanism for advancing the pressure in time. Consequently, much effort has been expended to eliminate the pressure from all or part of the computational process. We show a simple, natural way of doing this.
The incompressible Navier-Stokes equation is composite, the sum of two orthogonal equations,
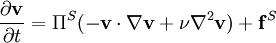 ,
,
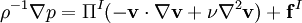 ,
,
where 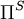 and
and 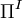 are solenoidal and irrotational projection operators satisfying
are solenoidal and irrotational projection operators satisfying 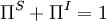 and
and
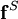 and
and 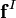 are the nonconservative and conservative parts of the body force. This result follows from the Helmholtz Theorem . The first equation is a pressureless governing equation for the velocity, while the second equation for the pressure is a functional of the velocity and is related to the pressure Poisson equation. The explicit functional forms of the projection operator in 2D and 3D are found from the Helmholtz Theorem, showing that these are integro-differential equations, and not particularly convenient for numerical computation.
are the nonconservative and conservative parts of the body force. This result follows from the Helmholtz Theorem . The first equation is a pressureless governing equation for the velocity, while the second equation for the pressure is a functional of the velocity and is related to the pressure Poisson equation. The explicit functional forms of the projection operator in 2D and 3D are found from the Helmholtz Theorem, showing that these are integro-differential equations, and not particularly convenient for numerical computation.
Equivalent weak or variational forms of the equations, proved to produce the same velocity solution as the Navier-Stokes equation are
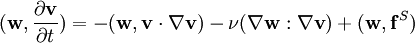 ,
,
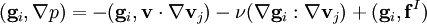 ,
,
for divergence-free test functions 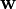 and irrotational test functions
and irrotational test functions 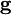 satisfying appropriate boundary conditions. Here, the projections are accomplished by the orthogonality of the solenoidal and irrotational function spaces. The discrete form of this is emminently suited to finite element computation of divergence-free flow.
satisfying appropriate boundary conditions. Here, the projections are accomplished by the orthogonality of the solenoidal and irrotational function spaces. The discrete form of this is emminently suited to finite element computation of divergence-free flow.
In the discrete case, it is desirable to choose basis functions for the velocity which reflect the essential feature of incompressible flow — the velocity elements must be divergence-free. While the velocity is the variable of interest, the existence of the stream function or vector potential is necessary by the Helmholtz Theorem. Further, to determine fluid flow in the absence of a pressure gradient, one can specify the difference of stream function values across a 2D channel, or the line integral of the tangential component of the vector potential around the channel in 3D, the flow being given by Stokes' Theorem. This leads naturally to the use of Hermite stream function (in 2D) or velocity potential elements (in 3D).
Involving, as it does, both stream function and velocity degrees-of-freedom, the method might be called a velocity-stream function or stream function-velocity method.
We now restrict discussion to a 3D continuous Hermite vector finite element which has first-derivative degrees-of-freedom. Taking the curl of the vector potential element gives a divergence-free velocity element [?][?]. The requirement that the vector potential element be continuous assures that the normal component of the velocity is continuous across element interfaces, all that is necessary for vanishing divergence on these interfaces.
Boundary conditions are simple to apply. The tangential component of the vector potential is constant on no-flow surfaces, with no-slip velocity conditions on surfaces. The line integral of the tangential component of the vector potential around ducts determine the flow. No boundary conditions are necessary on open boundaries [?], though consistent values may be used with some problems. These are all Dirichlet conditions.
The algebraic equations to be solved are simple to set up, but of course are non-linear, requiring iteration of the linearized equations.
The finite element we will use here has 48 degrees-of-freedom, six degrees-of-freedom at each of the eight nodes.
The code implementing the lid-driven cavity problem is written for Matlab. The script below is problem-specific, and calls problem-independent functions to evaluate the element diffusion and convection matricies and evaluate the pressure from the resulting velocity field. These three functions accept general convex hexahedral elements with planar faces, as well as the rectangular elements used here. Other functions are a GMRES iterative solver using ILU preconditioning and incorporating the essential boundary conditions, and a function to produce non-uniform nodal spacing for the problem mesh.
This "educational code" is a simplified version of code used in [?]. The user interface is the code itself. The user can experiment with changing the mesh, the Reynolds number, and the number of nonlinear iterations performed, as well as the relaxation factor. There are suggestions in the code regarding near-optimum choices for this factor as a function of Reynolds number. Some values are given in the paper as well. For larger Reynolds numbers, a smaller relaxation factor speeds up convergence by smoothing the velocity in the factor 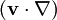 of the convection term, but will impede convergence if made too small.
of the convection term, but will impede convergence if made too small.
The output consists of graphic plots of contour levels of the stream function.
This simplified version for this Wiki resulted from removal of computation of a restart capability, comparison with published data, and production of publication-quality plots from the research codes used with the paper.
