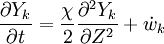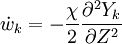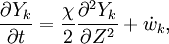Combustion
From CFD-Wiki
What is combustion -- Physics versus modelling
Combustion phenomena consists of many physical and chemical processes with broad range of time scales. Mathematical description of combustion is not always trivial. Analytical solutions exists only for basic situations of laminar flame and because of its assumptions it is often restricted to few problems solved usually in zero or one-dimensional space.
Problems solved today concern mainly turbulent flows, gas as well as liquid fuels, pollution issues (products of combustion as well as for example noise pollution). These problems require not only extensive experimental work, but also numerical modelling. All combustion models must be validated against the experiments as each one has its own drawbacks and limits. However here the modelling part will be mainly addressed.
Reaction mechanisms
The combustion is mainly chemical process and although we can, to some extend, describe flame without any chemistry informations, for modelling of flame propagation we need to know the speed of reactions, product concentrations, temperature and other parameters. Therefore more or less detailed information about reaction kinetics is essential for any combustion model. Mixture will generally combust, if the reaction of fuel and oxidiser is fast enough to maintain until all of the mixture is burned into products. If the reaction is too slow, the flame will extinguish, if too fast, explosion or even detonation will occur. The reaction rate of typical combustion reaction is influenced mainly by concentration of reactants, temperature and pressure.
A stoichiometric equation of an arbitrary equation can be written as:
|
|
where $\nu$ is the stoichiometric coefficient, 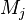 is arbitrary species. One
prime specifies the reactants and double prime products of the reaction.
is arbitrary species. One
prime specifies the reactants and double prime products of the reaction.
Reaction rate, expressing the rate of disappearance of reactant i of such a reaction, is defined as:
|
|
in which k is the specific reaction rate constant. Arrhenius found that this constant is a function only of temperature and this function is defined as:
|
|
where A is pre--exponential factor, E is activation energy and  is
temperature exponent.
These constants for given reactions can be found in literature.
The reaction mechanism can be given from experiments for every reaction
resolved, it could be also constructed numerically by automatic generation
method (see [Griffiths (1994)] for review on reaction mechanisms).
For simple hydrocarbon tens to hundreds of reactions are involved.
By analysis and systematic reduction of reaction mechanisms global reaction
(from one to five step reactions) can be found (see [Westbrook (1984)]).
is
temperature exponent.
These constants for given reactions can be found in literature.
The reaction mechanism can be given from experiments for every reaction
resolved, it could be also constructed numerically by automatic generation
method (see [Griffiths (1994)] for review on reaction mechanisms).
For simple hydrocarbon tens to hundreds of reactions are involved.
By analysis and systematic reduction of reaction mechanisms global reaction
(from one to five step reactions) can be found (see [Westbrook (1984)]).
Governing Equations for Reacting Flows
Together with the usual Navier-Stokes for compresible flows (See Governing Equations), additional equations are
needed in reacting flows.
The mass fraction transport equation for k-th species 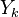 is:
is:
where Ficks law is assumed for scalar diffusion with 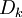 , the speices difussion coefficient and
, the speices difussion coefficient and 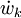 is the species reaction rate.
A non-reactive scalar (like the mixture fraction
is the species reaction rate.
A non-reactive scalar (like the mixture fraction 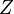 ) had the following transport equation:
) had the following transport equation:
where 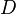 is the diffusion coefficient of the passive scalar.
is the diffusion coefficient of the passive scalar.
Infinitely fast chemistry
All combustion models can be divided into two main groups according to the assumptions on the reaction kinetics. We can either assume the reactions to be infinitely fast - compared to e.g. mixing of the species, or of the comparable time scale of the mixing process. The simpler approach assuming chemistry fast enough, that the limiting process is mixing of the species is historically older approach and even today can be appropriate approach. It is simpler to solve then #Finite rate chemistry models, but introduces errors to the solution which may or may not be important.
Premixed Combustion
Premixed flame occurs in mixtures of fuel and oxidiser, homogeneously premixed prior to the flame. These flames are not limited only to gas fuels, but also to the pre-vaporised fuels. Typical example of premixed laminar flame is bunsen burner, where the air enters the fuel stream. The mixture burns in the wake of the riser tube walls forming nice stable flame. The premixed flames has many advantages in terms of control of temperature and products and pollution concentration, but introduce also some dangers like the autoignition (in the supply system).
Turbulent flame speed model
Eddy Break-Up model
The Eddy Break-Up model is the typical example of mixed-is-burnt combustion model. It is based on the work of Magnussen and Hjertager, and Spalding and can be found in all CFD packages. The model assumes the reactions to be completed in the moment of mixing, so that the reaction rate is completely controlled by turbulent mixing. The combustion is described by a single step global chemical reaction:
|
|
in which F stands for fuel, O for oxidiser and P for products of the reaction. Alternativelly we can have multistep scheme, where each reaction has its own mean reaction rate. The mean reaction rate is given by:
|
|
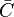 denotes mean concentrations for fuel, oxidiser and products
respectively, A and B are model constants with typical values of 0.5
and 4.0 respectively. The values of these constants are fitted according
to the experimental results and they are suitable for most of the general cases.
Still they are just constants based on experimental fitting and they need not
be suitable for all the situations.
Care must be taken especially in highly strained regions, where the ratio of
denotes mean concentrations for fuel, oxidiser and products
respectively, A and B are model constants with typical values of 0.5
and 4.0 respectively. The values of these constants are fitted according
to the experimental results and they are suitable for most of the general cases.
Still they are just constants based on experimental fitting and they need not
be suitable for all the situations.
Care must be taken especially in highly strained regions, where the ratio of  to
to  is large (flame-holder wakes, walls ...). In those regions a positive reaction rate occurs and an artificial flame can be observed.
CFD codes usually has some remedies to overcome this problem.
is large (flame-holder wakes, walls ...). In those regions a positive reaction rate occurs and an artificial flame can be observed.
CFD codes usually has some remedies to overcome this problem.
This model largely over-predicts temperatures and concentrations of species like CO and other species. Still this model is quite popular for its simplicity and relatively easy convergence and implementation.
Bray-Moss-Libby Model
Non premixed combustion
Conserved scalar equilibrium models
Finite rate chemistry
Premixed Combustion
Coherent Flame Model
Flamelets based on G equation
Non-premixed Combustion
Flamelets based on conserved scalar
Peters (2000) define Flamelets as "thin diffusion layers embedded in a turbulent non-reactive flow field".
If the chemistry is fast enough, the chemistry is active within a thin region
where the chemistry conditions are in (or close to) stoichiometric conditions, the "flame" surface.
This thin region is assumed to be smaller than Kolmogorov length scale and therefore the
region is locally laminar. The flame surface is defined as an iso-surface of a certain scalar 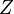 ,
mixture fraction in non-premixed combustion.
,
mixture fraction in non-premixed combustion.
The reactive problems is therefore split into two parts: First, the mixing , which consists of the location of the flame surface which is a non-reactive problem concerning the propagation of a passive scalar. And second, the flame structure , which deals with the distribution of the reactive species inside the flamelet.
To obtain the distribution inside the flame front we assume it is locally one-dimensional and depends only on time and the scalar coodinate.
Using the following chain rules for the time
and spatial coordinate
to the species transport equation (see Governing Equations for Reacting Flows) and re-arranging, we obtain
The second and third term in the LHS cancel due to continuity and mixture fraction transport, the equation therefore boils down to
where 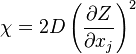 is called the scalar dissipation
and controls the mixing, providing the interaction between the flow and the chemistry.
is called the scalar dissipation
and controls the mixing, providing the interaction between the flow and the chemistry.
If the flame dependence on time is dropped, even though he field 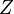 ) still depends on it.
) still depends on it.
This approach is called the Stationary Laminar Flamelet Model (SLFM) and has the advantage that libraries of
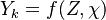 can be pre-computed and stored in look-up tables with all the required complex chemistry.
can be pre-computed and stored in look-up tables with all the required complex chemistry.
Flamelet Computation and Flamelet Libraries
The computation of non-premixed turbulent flames based on laminar-flamelet models is generally based on two-dimensional or three-dimensional CFD codes that employ standard models for fluid-mechanical closure of the govening equations. In many cases, for that purpose standard models such as the k-epsilon model are used, but occasionally more sophisticated models such as Reynolds-Stress models are also employed.
Chemical-source-term closure is a different matter. To this end, the CFD codes carry out suitable averaging procedures, such as pdf-avaraging on the basis of a beta function or a clipped Gaussian distribution. The quantities to be averaged are laminar-flamelet profiles, i.e., results from laminar-flamelet computations. Generally, these flamelet computations are carried oout a-priori, i.e, they are performed separately and prior to the turbulent-combustion simulation with the CFD code. Depending on the specific laminar-flamelet model used for the turbulent-combustion simulation, one or several parameters are varied in the laminat computatations. For instance, if the computations are based on
then the variable parameter is the scalar dissipation rate 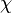 . The flamelet profiles for the various parameter values are stored in a dataset or file which is called
a "flamelet library". For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory COSILAB [1] with its relevant solver RUN1DL, which can be used for a variety of relevant geometries; see various
publications that are available for download.
. The flamelet profiles for the various parameter values are stored in a dataset or file which is called
a "flamelet library". For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory COSILAB [1] with its relevant solver RUN1DL, which can be used for a variety of relevant geometries; see various
publications that are available for download.
Conditional Moment Closure (CMC)
Multiple Mapping Closure (MMC)
Linear Eddy Model
PDF transport models
Lagrangian
Eulerian
References
- Griffiths J.F. (1994), "Reduced Kinetic Models and Their Application to Practical Combustion Systems", Prog. in Energy and Combustion Science,Vol. 21, pp. 25-107.
- Westbrook, Ch.K., Dryer,F.L., (1984), "Chemical Kinetic Modeling of Hydrocarbon Combustion", Prog. in Energy and Combustion Science,Vol. 10, pp. 1-57.

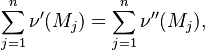
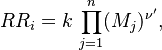
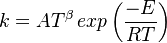
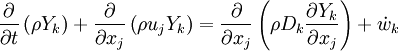
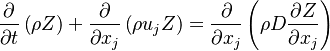
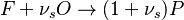
![\bar{\dot\omega}_F=A_{EB} \frac{\epsilon}{k}
min\left[\bar{C}_F,\frac{\bar{C}_O}{\nu},
B_{EB}\frac{\bar{C}_P}{(1+\nu)}\right]](/W/images/math/9/d/6/9d67c48a8dd1f2decb0d5bf3336d215b.png)
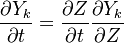
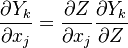
![\rho \frac{\partial Y_k}{\partial t} + Y_k \left[
\frac{\partial \rho}{\partial t} + \frac{\partial \rho u_j}{\partial x_j}
\right]
+ \frac{\partial Y_k}{\partial Z} \left[
\rho \frac{\partial Z}{\partial t} + \rho u_j \frac{\partial Z}{\partial x_j} -
\frac{\partial}{\partial x_j}\left( \rho D \frac{\partial Z}{\partial x_j} \right)
\right]
=
\rho D \left( \frac{\partial Z}{\partial x_j} \frac{\partial Z}{\partial x_j} \right) + \dot w_k](/W/images/math/e/2/9/e2921b67e8aadf42b355efe1f6cd8a19.png)