Dynamic subgrid-scale model
From CFD-Wiki
Contents |
Introduction
The limitations of the Smagorinsky model have lead to the formulation of more general subgrid-scale models. Perhaps the best known of these newer models is the dynamic subgrid-scale model (DSM) of Germano et al (1991). DSM may be viewed as a modification of the Smagorinsky model, as the dynamic model allows the Smagorinsky constant 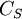 to vary in space and time.
to vary in space and time. 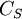 is calculated locally in each timestep based upon two filterings of the flow variables, which we
will denote by superscript
is calculated locally in each timestep based upon two filterings of the flow variables, which we
will denote by superscript 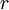 and superscript
and superscript 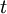 . These filters are called the grid filter and the test filter, respectively, and the test filter width is assumed to be larger the grid filter width.
. These filters are called the grid filter and the test filter, respectively, and the test filter width is assumed to be larger the grid filter width.
Original model
Filtering with the grid filter results in the normal LES equations, with 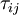 given by
given by
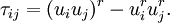
Filtering again with the test filter results in a similar set of equations, but with a different subgrid-scale stress term, given by
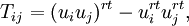
where the superscript 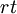 indicates grid filtering followed by test filtering. The two subgrid-scale stress terms are related by the Germano identity:
indicates grid filtering followed by test filtering. The two subgrid-scale stress terms are related by the Germano identity:
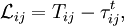
where
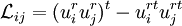
is the resolved turbulent stress. The Germano identity is used to calculate dynamic local values for 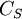 by applying the Smagorinsky model to both
by applying the Smagorinsky model to both 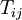 and
and 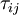 . The anisotropic part of
. The anisotropic part of 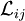 is the represented as
is the represented as
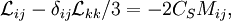
where
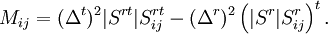
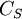 may now be computed as
may now be computed as
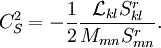
In practice, DSM requires stabilization. Often, this has been done by averaging
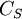 in a homogeneous direction. In cases where this is not possible, local averaging has been used in place of an average in a homogenous direction.
in a homogeneous direction. In cases where this is not possible, local averaging has been used in place of an average in a homogenous direction.
Alternate solution (Lilly)
Lilly (1991) proposed a least squares procedure that is generally preferred to the original calculation of 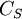 :
:
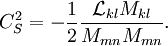
Stabilization must also be employed here as well.
References
- Germano, M., Piomelli, U., Moin, P. and Cabot, W. H. (1991), "A Dynamic Subgrid-Scale Eddy Viscosity Model", Physics of Fluids A, Vol. 3, No. 7, pp. 1760-1765.
- Lilly, D. K. (1991), "A Proposed Modification of the Germano Subgrid-Scale Closure Method", Physics of Fluids A, Vol. 4, No. 3, pp. 633-635.
