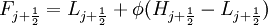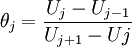Flux limiters
From CFD-Wiki
Continillo (Talk | contribs) (→References) |
|||
| (3 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | Most of us might have seen the behaviour of numerical schemes in order to capture shocks and discontinuity that arises in hyperbolic equations. Physically, these equations model the convective fluid flow. It has been observed that low-order schemes are usually stable but quite dissipative in nature around the points of discontinuity/shocks. On the other hand higher-order numerical schemes are unstable in nature and show oscillations in the vicinity of discontinuity. One can have a | + | Most of us might have seen the behaviour of numerical schemes in order to capture shocks and discontinuity that arises in hyperbolic equations. Physically, these equations model the convective fluid flow. It has been observed that low-order schemes are usually stable but quite dissipative in nature around the points of discontinuity/shocks. On the other hand higher-order numerical schemes are unstable in nature and show oscillations in the vicinity of discontinuity. One can have a better understanding of such behaviour by analysing the modified equation of these schemes. |
| - | + | Now as said above one can not have high order accuracy without oscillations. The objective is to have highly accurate and stable oscillation free schemes. This kind of schemes are known as high resolution schemes. In 1984 Harten proposed the constuction and gave TVD criteria for such scheme. Here we talk only about using flux limiters function to construct high resolution schemes. The idea is to tune the numerical flux of high order and low order scheme using the flux limiter function in such a way that the resulting scheme gives a high order accuracy in the smooth region of flow and sticks with first order of accuracy in the vicinity of socks/discontinuities as follows: | |
Define the numerical flux fuction of high resolution conservative scheme as | Define the numerical flux fuction of high resolution conservative scheme as | ||
| - | <math>F_{j+ \frac{1}{2}} = L_{j+\frac{1}{2}} + \phi(H_{j+ \frac{1}{2}} - L_{j+ \frac{1}{2}})</math> | + | |
| + | :<math>F_{j+ \frac{1}{2}} = L_{j+\frac{1}{2}} + \phi(H_{j+ \frac{1}{2}} - L_{j+ \frac{1}{2}})</math> | ||
| + | |||
where <math>L, H</math> are the numerical flux of conservative low order and high order schemes respectively. | where <math>L, H</math> are the numerical flux of conservative low order and high order schemes respectively. | ||
| - | and <math>\phi</math> is a function of smoothness parameter <math>\theta</math> defined | + | and <math>\phi</math> is a function of smoothness parameter <math>\theta</math> usually defined as |
| - | What remains next is to define the limiter fuction <math>\phi(\theta)</math> in such a way that it satisfies at least the following: | + | |
| - | + | :<math>\theta_j = \frac{U_j -U_{j-1}}{U_{j+1} - U{j}}</math> | |
| - | + | ||
| - | + | What remains next is to define the limiter fuction <math>\phi(\theta)</math> in such a way that it satisfies at least the following properties: | |
| - | + | ||
| - | + | * remains positive <math>\forall \theta</math>, | |
| + | * satisfies <math> \phi(1) = 1</math> | ||
| + | * passes through a perticular region known as TVD region associted with the underlying scheme in order to guarantee stability of the scheme. | ||
| - | + | ==References== | |
| - | + | * C. B. Laney, "Computational Gas Dynamics" | |
| - | C. B. Laney | + | * E. F. Toro, "Riemann Solvers and Numerical Methods for Fluid Dynamics" |
| + | * R. J. Leveque, "Numerical Methods for Conservation Laws" | ||
Latest revision as of 10:19, 22 February 2007
Most of us might have seen the behaviour of numerical schemes in order to capture shocks and discontinuity that arises in hyperbolic equations. Physically, these equations model the convective fluid flow. It has been observed that low-order schemes are usually stable but quite dissipative in nature around the points of discontinuity/shocks. On the other hand higher-order numerical schemes are unstable in nature and show oscillations in the vicinity of discontinuity. One can have a better understanding of such behaviour by analysing the modified equation of these schemes.
Now as said above one can not have high order accuracy without oscillations. The objective is to have highly accurate and stable oscillation free schemes. This kind of schemes are known as high resolution schemes. In 1984 Harten proposed the constuction and gave TVD criteria for such scheme. Here we talk only about using flux limiters function to construct high resolution schemes. The idea is to tune the numerical flux of high order and low order scheme using the flux limiter function in such a way that the resulting scheme gives a high order accuracy in the smooth region of flow and sticks with first order of accuracy in the vicinity of socks/discontinuities as follows:
Define the numerical flux fuction of high resolution conservative scheme as
where 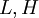 are the numerical flux of conservative low order and high order schemes respectively.
and
are the numerical flux of conservative low order and high order schemes respectively.
and 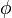 is a function of smoothness parameter
is a function of smoothness parameter 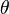 usually defined as
usually defined as
What remains next is to define the limiter fuction 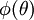 in such a way that it satisfies at least the following properties:
in such a way that it satisfies at least the following properties:
- remains positive
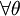 ,
,
- satisfies
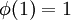
- passes through a perticular region known as TVD region associted with the underlying scheme in order to guarantee stability of the scheme.
References
- C. B. Laney, "Computational Gas Dynamics"
- E. F. Toro, "Riemann Solvers and Numerical Methods for Fluid Dynamics"
- R. J. Leveque, "Numerical Methods for Conservation Laws"