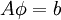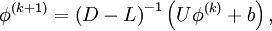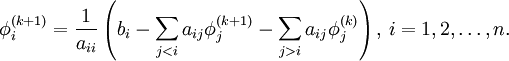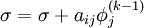Gauss-Seidel method
From CFD-Wiki
m |
m (mainly corrections) |
||
| Line 8: | Line 8: | ||
:<math> | :<math> | ||
| - | \phi^{(k)} = \left( {D - L} \right)^{ - 1} \left( {U\phi^{(k | + | \phi^{(k+1)} = \left( {D - L} \right)^{ - 1} \left( {U\phi^{(k)} + b} \right), |
</math> | </math> | ||
| Line 14: | Line 14: | ||
:<math> | :<math> | ||
| - | \phi^{(k)}_i = \frac{1}{a_{ii}} \left(b_i - \sum_{j<i}a_{ij}\phi^{(k+1)}_j-\sum_{j>i}a_{ij}\phi^{(k)}_j\right),\, i=1,2,\ldots,n. | + | \phi^{(k+1)}_i = \frac{1}{a_{ii}} \left(b_i - \sum_{j<i}a_{ij}\phi^{(k+1)}_j-\sum_{j>i}a_{ij}\phi^{(k)}_j\right),\, i=1,2,\ldots,n. |
</math> | </math> | ||
| - | Note that the computation of <math>\phi^{(k)}_i</math> uses only those elements of <math>\phi^{(k+1)}</math> that have already been computed. This means that no additional storage is required, and the computation can be done in place (<math>\phi^{(k+1)}</math> replaces <math>\phi^{(k)}</math>). While this might seem like a rather minor concern, for large systems it is unlikely that every iteration can be stored. Thus, unlike the [[Jacobi method]], we do not have to do any vector copying should we wish to use only one storage vector. The iteration is generally continued until the changes made by an iteration are below some tolerance. | + | Note that the computation of <math>\phi^{(k+1)}_i</math> uses only those elements of <math>\phi^{(k+1)}</math> that have already been computed. This means that no additional storage is required, and the computation can be done in place (<math>\phi^{(k+1)}</math> replaces <math>\phi^{(k)}</math>). While this might seem like a rather minor concern, for large systems it is unlikely that every iteration can be stored. Thus, unlike the [[Jacobi method]], we do not have to do any vector copying should we wish to use only one storage vector. The iteration is generally continued until the changes made by an iteration are below some tolerance. |
== Algorithm == | == Algorithm == | ||
Revision as of 01:09, 19 December 2005
Introduction
We seek the solution to set of linear equations:
In matrix terms, the the Gauss-Seidel iteration can be expressed as
where 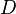 ,
, 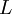 and
and 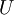 represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix
represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix 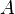 and
and 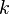 is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used:
is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used:
Note that the computation of 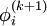 uses only those elements of
uses only those elements of 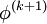 that have already been computed. This means that no additional storage is required, and the computation can be done in place (
that have already been computed. This means that no additional storage is required, and the computation can be done in place (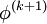 replaces
replaces 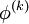 ). While this might seem like a rather minor concern, for large systems it is unlikely that every iteration can be stored. Thus, unlike the Jacobi method, we do not have to do any vector copying should we wish to use only one storage vector. The iteration is generally continued until the changes made by an iteration are below some tolerance.
). While this might seem like a rather minor concern, for large systems it is unlikely that every iteration can be stored. Thus, unlike the Jacobi method, we do not have to do any vector copying should we wish to use only one storage vector. The iteration is generally continued until the changes made by an iteration are below some tolerance.
Algorithm
- Chose an initial guess
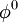
- for k := 1 step 1 until convergence do
- for i := 1 step until n do
-
- for j := 1 step until i-1 do
-
- end (j-loop)
- for j := i+1 step until n do
-
- end (j-loop)
-
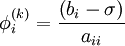
-
- end (i-loop)
- check if convergence is reached
- for i := 1 step until n do
- end (k-loop)