Gresho vortex
From CFD-Wiki
Contents |
Classical Definition
The Gresho problem [1] is a rotating vortex problem independent of time for the case of inviscid flow (Euler equations). Angular velocity 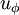 depends only on radius and the centrifugal force is balanced by the gradient of the pressure
depends only on radius and the centrifugal force is balanced by the gradient of the pressure 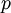 .
.
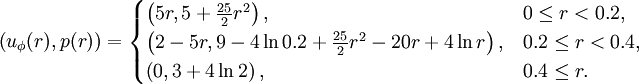
The radial velocity is zero and the density is one everywhere.
Furthermore, we can modify this setup and let the vortex move with constant velocity. Customarily, we use periodic boundary conditions in each direction.
Dependence on Mach number
Miczek [2] modified the setup by introducing a reference Mach number. Pressure is scaled such that the rotation acts on this Mach number.
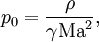
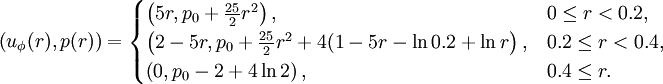
Now, we can use the Gresho vortex as test case how well the numerical scheme performs in dependence of the Mach number.
Properties and Applications
In the original formulation, the Gresho vortex is a test for the following properties [1,3]:
- Accuracy of numerical scheme: the empirical order of accuracy is around 1.4 for this problem.
- Preservation of symmetry: since the analytical solution is pure rotation, the vortex should not change its shape.
- Conservation of angular momentum: the smoothing of the azimuthal velocity profile is a measure how well the code preserves angular momentum.
Furthermore, [3] for the case of Voronoi meshes and [4] for curvilinear grids use the Gresho vortex to check the errors arising from the chosen numerical grid.
The modified version from [2] can be used to check the ability of the numerical scheme to handle low Mach number flows [2,4,5]. For small Mach numbers, the numerical dissipation of many finite difference schemes will lead to strong deformations of the vortex.
References
[1] Liska R., Wendroff B. Comparison of Several Difference Schemes on 1D and 2D Test Problems for the Euler Equations. SIAM J. Sci. Comput., 25(3), 995–1017 (23 pages).
[2] Miczek F. Simulation of low Mach number astrophysical flows. München, Technische Universität München, Diss., 2013.
[3] Springel V. E pur si muove: Galilean-invariant cosmological hydrodynamical simulations on a moving mesh. Mon. Not. R. Astron. Soc. 401, 791–851 (2010).
[4] Grimm-Strele H., Kupka F., Muthsam H. Curvilinear Grids for WENO Methods in Astrophysical Simulations. Submitted to Computer Physics Communications, 2013.
[5] Happenhofer N., Grimm-Strele H., Kupka F., Löw-Baselli B., Muthsam H. A low Mach number solver: Enhancing applicability. Journal of Computational Physics Volume 236, 1 March 2013, Pages 96-118.

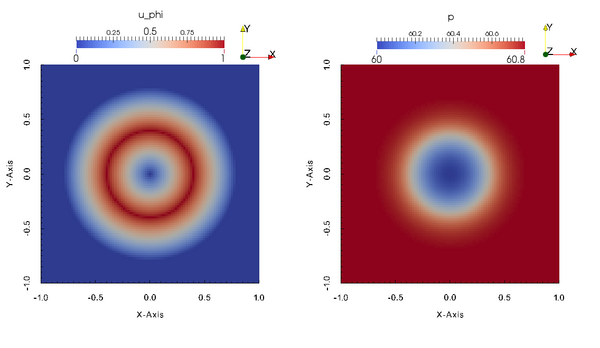
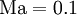 . Here, the computational domain is
. Here, the computational domain is ![[-1,1] \times [-1,1]](/W/images/math/a/f/d/afd6932f58971a6eabd42f45e3009223.png) and the Gresho vortex was stretched by a factor 2.
and the Gresho vortex was stretched by a factor 2.