Introduction to numerical methods
From CFD-Wiki
| Line 24: | Line 24: | ||
== Simple Flows == | == Simple Flows == | ||
=== [[Incompressible flow]] === | === [[Incompressible flow]] === | ||
| - | === [[Euler or inviscid flow]] === | + | === [[Inviscid flow | Euler or inviscid flow]] === |
=== [[Potential flow]] === | === [[Potential flow]] === | ||
| - | === [[Stokes or creeping flow]] === | + | === [[Stokes flow | Stokes or creeping flow]] === |
---- | ---- | ||
<i> Return to [[Numerical methods | Numerical Methods]] </i> | <i> Return to [[Numerical methods | Numerical Methods]] </i> | ||
Revision as of 09:45, 5 October 2005
Fluids could be regarded as substances those on application of external force deform or show very little resistance to deformation. This deformation in the cases of liquid and gases is substantial. Both obey common lows of motion and both for most practical computational purposes can be regarded as continuum. Forces can be considered as body forces, example: forces due to gravity or they can be considered as surface forces example: surface tension.
Based on speed and nature of flow, flows could be categorized into:
Based upon their Mach number. This Mach number could be used to determine whether the flow shall be considered as Incompressible flow or Compressible flow for computational purposes. For the flows of Mach number smaller than 0.3, we can safely assume them as incompressible for all computational purposes.
Based upon the degree of effect upon the viscosity on the flow, the flows could be classified as Viscous flow or Inviscid flow in nature. Fluids obeying Newton’s law are called Newtonian fluids. Further based upon the phases of flow, the flows can be considered as multiphase or single phase flows.
Contents |
Control Volume Approach
Conservation laws can be applied to given quantity of fluid. However, it is more convenient to apply them on a small spatial region, called Control volume. For this purposes the geometry under consideration is subdivided into smaller sub-regions. Together they are called mesh or grid. And the approach used is called Control volume approach for solving the flow problem.
The figure 1.1 shows one such computational domain.
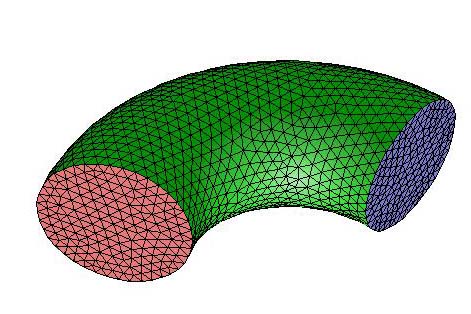
Figure 1.1
Conservation Principles
Conservation of scalar quantities
Simple Flows
Incompressible flow
Euler or inviscid flow
Potential flow
Stokes or creeping flow
Return to Numerical Methods
