Introduction to turbulence/Statistical analysis/Generalization to the estimator of any quantity
From CFD-Wiki
Similar relations can be formed for the estimator of any function of the random variable say 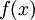 . For example, an estimator for the average of
. For example, an estimator for the average of 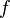 based on
based on 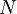 realizations is given by:
realizations is given by:
|
| (2) |
where 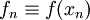 . It is straightforward to show that this estimator is unbiased, and its variability (squared) is given by:
. It is straightforward to show that this estimator is unbiased, and its variability (squared) is given by:
|
| (2) |
Example: Suppose it is desired to estimate the variability of an estimator for the variance based on a finite number of samples as:
|
| (2) |
(Note that this estimator is not really very useful since it presumes that the mean value, 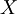 , is known, whereas in fact usually only
, is known, whereas in fact usually only 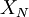 is obtainable).
is obtainable).
Answer
Let 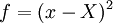 in equation 2.55 so that
in equation 2.55 so that 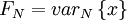 ,
, 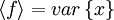 and
and ![var \left\{f \right\} = var \left\{ \left( x-X \right)^{2} - var \left[ x-X \right] \right\}](/W/images/math/4/9/0/490a881ef051ed37db7bccb8888989bf.png) . Then:
. Then:
| (2) |
This is easiest to understand if we first expand only the numerator to oblain:
|
| (2) |
Thus
|
| (2) |

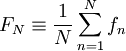
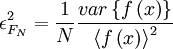
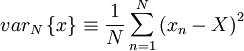
![var \left\{ \left( x- X \right)^{2} - var\left[x \right] \right\} = \left\langle \left( x- X \right)^{4} \right\rangle - \left[ var \left\{ x \right\} \right]^2](/W/images/math/f/d/a/fda59399bb14995d4520dc7b52f09efe.png)
![\epsilon^{2}_{var_{N}} = \frac{\left\langle \left( x- X \right)^4 \right\rangle}{\left[ var \left\{ x \right\} \right]^2 } - 1](/W/images/math/c/9/3/c93659bc771b229cc583b07ce8d97312.png)