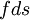Introduction to turbulence/Statistical analysis/Probability
From CFD-Wiki
(→The histogram and probability density function) |
(→The histogram and probability density function) |
||
| Line 5: | Line 5: | ||
The frequency of occurence of a given ''amplitude'' (or value) from a finite number of realizations of a random variable can be displayed by dividing the range of possible values of the random variables into a number of slots (or windows). Since all possible values are covered, each realization fits into only one window. For every realization a count is entered into the appropriate window. When all the realizations have been considered, the number of counts in each window is divided by the total number of realizations. The result is called the '''histogram''' (or ''frequency of occurence'' diagram). From the definitioin it follows immediately that the sum of the values of all the windows is exactly one. | The frequency of occurence of a given ''amplitude'' (or value) from a finite number of realizations of a random variable can be displayed by dividing the range of possible values of the random variables into a number of slots (or windows). Since all possible values are covered, each realization fits into only one window. For every realization a count is entered into the appropriate window. When all the realizations have been considered, the number of counts in each window is divided by the total number of realizations. The result is called the '''histogram''' (or ''frequency of occurence'' diagram). From the definitioin it follows immediately that the sum of the values of all the windows is exactly one. | ||
| - | The shape of a histogram depends on the ''statistical distribution of the random variable'', but it also depends on the total number of realizations, ''N'', and the size of the slots, <math> \Delta c </math>. THe histogram can be represented symbolically by the function <math> H_{x}(c,\Delta c,N)</math> where <math> c\leq x \triangleleft c + \Delta c </math>, <math> \Delta c </math> is the slot width, and <math> N </math> is the number of realizaions of the random variable. Thus the histogram shows the relative frequency of occurence of a given value range in a given ensemble. Figure 2.3 illustrates a typical histogram. If the size of the sample is increased so that the number of realizations in each | + | The shape of a histogram depends on the ''statistical distribution of the random variable'', but it also depends on the total number of realizations, ''N'', and the size of the slots, <math> \Delta c </math>. THe histogram can be represented symbolically by the function <math> H_{x}(c,\Delta c,N)</math> where <math> c\leq x \triangleleft c + \Delta c </math>, <math> \Delta c </math> is the slot width, and <math> N </math> is the number of realizaions of the random variable. Thus the histogram shows the relative frequency of occurence of a given value range in a given ensemble. Figure 2.3 illustrates a typical histogram. If the size of the sample is increased so that the number of realizations in each window increases, the diagram will become less erratic and will be more representative of the actual ''probability'' of occurence of the amplitudes of the signal itself, as long as the window size is sufficiently small. |
| + | |||
| + | If the number of realizations, <math> N </math>, increases without bound as the window size, <math> \Delta c </math> , goes to zero, the histogram divided by the window size goes to a limiting curve called the probability density function, <math> B_{x} \left( c \right) </math>. That is, | ||
| + | |||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | :<math> | ||
| + | fds | ||
| + | </math> | ||
| + | </td><td width="5%">(2)</td></tr></table> | ||
=== The probability distribution === | === The probability distribution === | ||
Revision as of 09:46, 29 May 2006
Contents |
Probability
The histogram and probability density function
The frequency of occurence of a given amplitude (or value) from a finite number of realizations of a random variable can be displayed by dividing the range of possible values of the random variables into a number of slots (or windows). Since all possible values are covered, each realization fits into only one window. For every realization a count is entered into the appropriate window. When all the realizations have been considered, the number of counts in each window is divided by the total number of realizations. The result is called the histogram (or frequency of occurence diagram). From the definitioin it follows immediately that the sum of the values of all the windows is exactly one.
The shape of a histogram depends on the statistical distribution of the random variable, but it also depends on the total number of realizations, N, and the size of the slots, 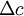 . THe histogram can be represented symbolically by the function
. THe histogram can be represented symbolically by the function 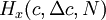 where
where 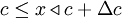 ,
, 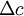 is the slot width, and
is the slot width, and 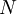 is the number of realizaions of the random variable. Thus the histogram shows the relative frequency of occurence of a given value range in a given ensemble. Figure 2.3 illustrates a typical histogram. If the size of the sample is increased so that the number of realizations in each window increases, the diagram will become less erratic and will be more representative of the actual probability of occurence of the amplitudes of the signal itself, as long as the window size is sufficiently small.
is the number of realizaions of the random variable. Thus the histogram shows the relative frequency of occurence of a given value range in a given ensemble. Figure 2.3 illustrates a typical histogram. If the size of the sample is increased so that the number of realizations in each window increases, the diagram will become less erratic and will be more representative of the actual probability of occurence of the amplitudes of the signal itself, as long as the window size is sufficiently small.
If the number of realizations, 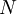 , increases without bound as the window size,
, increases without bound as the window size, 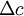 , goes to zero, the histogram divided by the window size goes to a limiting curve called the probability density function,
, goes to zero, the histogram divided by the window size goes to a limiting curve called the probability density function, 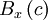 . That is,
. That is,
|
| (2) |
The probability distribution
dfsgdsfg
Gaussian (or normal) distributions
fdgdsgadfg