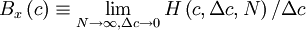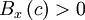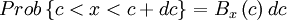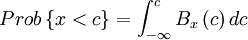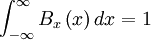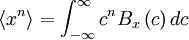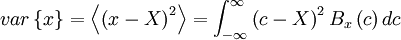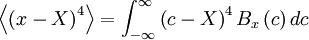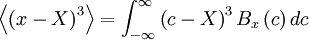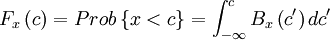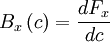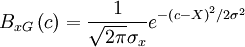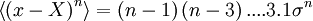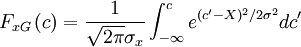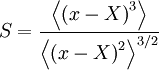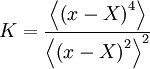Introduction to turbulence/Statistical analysis/Probability
From CFD-Wiki
(→The histogram and probability density function) |
Ayyoubzadeh (Talk | contribs) (→Skewness and kurtosis) |
||
| (40 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | == | + | {{Introduction to turbulence menu}} |
| + | == The histogram and probability density function == | ||
| - | + | The frequency of occurrence of a given ''amplitude'' (or value) from a finite number of realizations of a random variable can be displayed by dividing the range of possible values of the random variables into a number of slots (or windows). Since all possible values are covered, each realization fits into only one window. For every realization a count is entered into the appropriate window. When all the realizations have been considered, the number of counts in each window is divided by the total number of realizations. The result is called the '''histogram''' (or ''frequency of occurrence'' diagram). From the definition it follows immediately that the sum of the values of all the windows is exactly one. | |
| - | The | + | The shape of a histogram depends on the ''statistical distribution of the random variable'', but it also depends on the total number of realizations, ''N'', and the size of the slots, <math> \Delta c </math>. The histogram can be represented symbolically by the function <math> H_{x}(c,\Delta c,N)</math> where <math> c\leq x < c + \Delta c </math>, <math> \Delta c </math> is the slot width, and <math> N </math> is the number of realizations of the random variable. Thus the histogram shows the relative frequency of occurrence of a given value range in a given ensemble. <font color="orange">Figure 2.3</font> illustrates a typical histogram. If the size of the sample is increased so that the number of realizations in each window increases, the diagram will become less erratic and will be more representative of the actual ''probability'' of occurrence of the amplitudes of the signal itself, as long as the window size is sufficiently small. |
| - | + | <font color="orange" size="3">Figure 2.3 not uploaded yet</font> | |
If the number of realizations, <math> N </math>, increases without bound as the window size, <math> \Delta c </math> , goes to zero, the histogram divided by the window size goes to a limiting curve called the probability density function, <math> B_{x} \left( c \right) </math>. That is, | If the number of realizations, <math> N </math>, increases without bound as the window size, <math> \Delta c </math> , goes to zero, the histogram divided by the window size goes to a limiting curve called the probability density function, <math> B_{x} \left( c \right) </math>. That is, | ||
| + | :<math> | ||
| + | B_{x} \left( c \right) \equiv \lim_{{ N \rightarrow \infty}, \Delta c \rightarrow 0} H \left( c , \Delta c , N \right) / \Delta c | ||
| + | </math> | ||
| + | |||
| + | Note that as the window width goes to zero, so does the number of realizations which fall into it, <math> N H </math>. Thus it is only when this number (or relative number) is divided by the slot width that a meaningful limit is achieved. | ||
| + | |||
| + | The '''probability density function''' (or '''pdf''') has the following properties: | ||
| + | |||
| + | * Property 1: | ||
| + | |||
| + | :<math>B_{x} \left( c \right) > 0</math> | ||
| + | |||
| + | always. | ||
| + | |||
| + | * Property 2: | ||
| + | |||
| + | :<math>Prob \left\{c < x < c + dc \right\} = B_{x} \left(c \right) dc</math> | ||
| + | |||
| + | where <math> Prob \left\{ \right\}</math> is read "the probability that". | ||
| + | |||
| + | * Property 3: | ||
| + | |||
| + | :<math>Prob \left\{ x < c \right\} = \int ^{c}_{- \infty }B_{x} \left(c \right) dc</math> | ||
| + | |||
| + | * Property 4: | ||
| + | |||
| + | :<math>\int ^{\infty}_{- \infty }B_{x} \left(x \right) dx = 1</math> | ||
| + | |||
| + | The condition imposed by property (1) simply states that negative probabilities are impossible, while property (4) assures that the probability is unity that a realization takes on some value. Property (2) gives the probability of finding the realization in a interval around a certain value, while property (3) provides the probability that the realization is less than a prescribed value. Note the necessity of distinguishing between the running variable, <math> x </math> , and the integration variable, <math> c </math>, in property (2) and (3). | ||
| + | |||
| + | Since <math> B_{x} \left( c \right) dc </math> gives the probability of the random variable <math> x </math> assuming a value between <math> c </math> and <math> c + dc </math>, any moment of the distribution can be computed by integrating the appropriate power of <math> x </math> over all possible values. Thus the <math> n </math> - th moment is given by: | ||
| - | |||
:<math> | :<math> | ||
| - | + | \left\langle x^{n} \right\rangle = \int^{\infty}_{- \infty} c^{n} B_{x} \left(c \right) dc | |
</math> | </math> | ||
| - | |||
| - | == | + | '''Exercise:''' Show (by returning to the definitions) that the value of the moment determined in this manner is exactly equal to the ensemble average defined earlier in the definition of the <math>m</math>-th moment. (Hint: use the definition of an integral as a limiting sum.) |
| + | |||
| + | If the probability density is given, the moments of all orders can be determined. For example, the variance can be determined by: | ||
| + | |||
| + | :<math> | ||
| + | var \left\{ x \right\} = \left\langle \left( x - X \right)^2 \right\rangle = \int^{\infty}_{- \infty} \left(c - X \right)^2 B_{x} \left(c \right) dc | ||
| + | </math> | ||
| + | |||
| + | The central moments give information about the shape of the probability density function, and ''vice versa''. <font color="orange">Figure 2.4</font> shows three distributions which have the same mean and standard deviation, but are clearly quite different. Beneath them are shown random functions of time, which might have generated them. Distribution (b) has a higher value of the fourth central moment than does distribution (a). This can be easily seen from the definition | ||
| + | |||
| + | <font color="orange" size="3">Figure 2.4 not uploaded yet</font> | ||
| + | |||
| + | :<math> | ||
| + | \left\langle \left( x - X \right)^{4} \right\rangle = \int^{\infty}_{- \infty} \left(c - X \right)^4 B_{x} \left(c \right) dc | ||
| + | </math> | ||
| + | |||
| + | since the fourth power emphasizes the fact that distribution (b) has more weight in the tails than does distribution (a). | ||
| + | |||
| + | It is also easy to see that because of the symmetry of pdf's in (a) and (b) all the odd central moments will be zero. Distributions (c) and (d), on the other hand, have non-zero values for the odd moments, because of their asymmtry. For example, | ||
| + | |||
| + | :<math> | ||
| + | \left\langle \left( x - X \right)^{3} \right\rangle = \int^{\infty}_{- \infty} \left(c - X \right)^3 B_{x} \left(c \right) dc | ||
| + | </math> | ||
| + | |||
| + | is equal to zero if <math> B_{x} </math> is an even function. | ||
| + | |||
| + | == The probability distribution == | ||
| - | + | Sometimes it is convienient to work with the '''probability distribution''' instead of with probability density function. The probability distribution is defined as the probability that the random variable has a value less than or equal to a given value. Thus from the equation for property (3), the probability distribution is given by | |
| + | |||
| + | :<math> | ||
| + | F_{x} \left( c \right) = Prob \left\{ x < c \right\} = \int^{c}_{-\infty} B_{x} \left( c' \right) d c' | ||
| + | </math> | ||
| + | |||
| + | Note that we had to introduce the integration variable, <math> c' </math>, since <math> c </math> occured in the limits. | ||
| + | |||
| + | This equation can be inverted by differentiating by <math> c </math> to obtain | ||
| + | |||
| + | :<math> | ||
| + | B_{x} \left( c \right) = \frac{dF_{x}}{dc} | ||
| + | </math> | ||
| + | |||
| + | == Gaussian (or normal) distributions == | ||
| + | |||
| + | One of the most important pdf's in turbulence is the Gaussian or Normal distribution defined by | ||
| + | |||
| + | :<math> | ||
| + | B_{xG} \left( c \right) = \frac{1}{\sqrt{2\pi} \sigma_{x}} e^{-\left( c - X \right)^{2} / 2 \sigma^{2} } | ||
| + | </math> | ||
| + | |||
| + | where <math>X</math> is the mean and <math> \sigma </math> is the standard derivation. The factor <math> 1 / \sqrt{2\pi} \sigma_{x}</math> insures that the integral of the pdf ocer all values is unity as required. It is easy to prove that this is the case by completing the squares in the integration of the exponential. | ||
| + | |||
| + | The Gaussian distribution is unusual in that it is completely determined by its first two moments, <math>X</math> and <math> \sigma </math>. This is ''not'' typical of most turbulence distributions. Nonetheless, it is sometimes useful to approximate turbulence as being Gaussian, often because of the absence of simple alternatives. | ||
| + | |||
| + | It is straightforward to show by integrating by parts that all the even central moments above the second are given by the following recursive relationship, | ||
| + | |||
| + | :<math> | ||
| + | \left\langle \left( x - X \right)^{n} \right\rangle = \left( n - 1 \right) \left( n - 3 \right) ....3.1 \sigma^{n} | ||
| + | </math> | ||
| + | |||
| + | Thus the fourth central moment is <math> 3 \sigma^{4} </math> the sixth is <math> 15 \sigma^{6} </math>, and so forth. | ||
| + | |||
| + | '''Exercise:''' Prove this: The probability distribution corresponding to the Gaussian distribution can be obtained by integrating the Gaussian pdf from <math>- \infty</math> to <math>x = c</math>; i.e., | ||
| + | |||
| + | :<math> | ||
| + | F_{xG} \left( c \right) = | ||
| + | \frac{1}{\sqrt{2\pi} \sigma_{x}} | ||
| + | \int^{c}_{- \infty} | ||
| + | e^{(c' - X)^2 / 2 \sigma^2} dc' | ||
| + | </math> | ||
| + | |||
| + | The integral is related to the erf-function tabulated in many standard tables. | ||
| + | |||
| + | == Skewness and kurtosis == | ||
| + | |||
| + | Because of their importance in characterizing the shape of the pdf, it is useful to definescaled versions of third and fourth central moments, the ''skewness'' and ''kurtosis'' respectively. The ''skewness'' is defined as third central moment divided by three*halves of the second; i.e. | ||
| + | |||
| + | :<math> | ||
| + | S = \frac{\left\langle \left( x- X \right)^{3} \right\rangle }{ \left\langle \left( x- X \right)^{2} \right\rangle^{3/2} } | ||
| + | </math> | ||
| + | |||
| + | The ''kurtosis'' defined as the fourth central moment divided by the square of the second; i.e. | ||
| + | |||
| + | :<math> | ||
| + | K = \frac{\left\langle \left( x- X \right)^{4} \right\rangle }{ \left\langle \left( x- X \right)^{2} \right\rangle^{2} } | ||
| + | </math> | ||
| + | |||
| + | Both these are easy to remember if you note the <math>S</math> and <math>K</math> must be dimensionless. | ||
| + | |||
| + | The pdf's in <font color="orange">Figure 2.4</font> can be distinguished by means of their skewness and kurtosis. The random variable shown in (b) has a higher kurtosis than that in (a). Thus the kurtosis can be used as an indication of the tails of a pdf, a higher kurtosis indicating that relatively larger excursions from the mean are more probable. The skewness of (a) and (b) are zero, whereas those for (c) and (d) are non-zero. Thus, as its name implies, a non-zero skewness indicates a skewed or asymmetric pdf, which in turn means that larger excursions in one direction are more probable than in the other. For a Gaussian pdf, the skewness is zero and then kurtosis is equal to three. The flatness factor, defined as <math>( K-3 )</math>, is sometimes used to indicate deviations from Gaussian behavior. | ||
| + | |||
| + | '''Exercise:''' Prove that the kurtosis of a Gaussian distributed random variable is 3. | ||
| + | |||
| + | {| class="toccolours" style="margin: 2em auto; clear: both; text-align:center;" | ||
| + | |- | ||
| + | | [[Statistical analysis in turbulence|Up to statistical analysis]] | [[Ensemble average in turbulence|Back to ensemble average]] | [[Multivariate random variables|Forward to multivariate random variables]] | ||
| + | |} | ||
| - | + | {{Turbulence credit wkgeorge}} | |
| - | + | {{Chapter navigation|Ensemble average|Multivariate random variables}} | |
Latest revision as of 16:30, 31 August 2007
Contents |
The histogram and probability density function
The frequency of occurrence of a given amplitude (or value) from a finite number of realizations of a random variable can be displayed by dividing the range of possible values of the random variables into a number of slots (or windows). Since all possible values are covered, each realization fits into only one window. For every realization a count is entered into the appropriate window. When all the realizations have been considered, the number of counts in each window is divided by the total number of realizations. The result is called the histogram (or frequency of occurrence diagram). From the definition it follows immediately that the sum of the values of all the windows is exactly one.
The shape of a histogram depends on the statistical distribution of the random variable, but it also depends on the total number of realizations, N, and the size of the slots, 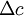 . The histogram can be represented symbolically by the function
. The histogram can be represented symbolically by the function 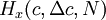 where
where 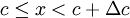 ,
, 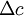 is the slot width, and
is the slot width, and 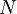 is the number of realizations of the random variable. Thus the histogram shows the relative frequency of occurrence of a given value range in a given ensemble. Figure 2.3 illustrates a typical histogram. If the size of the sample is increased so that the number of realizations in each window increases, the diagram will become less erratic and will be more representative of the actual probability of occurrence of the amplitudes of the signal itself, as long as the window size is sufficiently small.
is the number of realizations of the random variable. Thus the histogram shows the relative frequency of occurrence of a given value range in a given ensemble. Figure 2.3 illustrates a typical histogram. If the size of the sample is increased so that the number of realizations in each window increases, the diagram will become less erratic and will be more representative of the actual probability of occurrence of the amplitudes of the signal itself, as long as the window size is sufficiently small.
Figure 2.3 not uploaded yet
If the number of realizations, 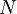 , increases without bound as the window size,
, increases without bound as the window size, 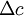 , goes to zero, the histogram divided by the window size goes to a limiting curve called the probability density function,
, goes to zero, the histogram divided by the window size goes to a limiting curve called the probability density function, 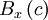 . That is,
. That is,
Note that as the window width goes to zero, so does the number of realizations which fall into it, 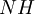 . Thus it is only when this number (or relative number) is divided by the slot width that a meaningful limit is achieved.
. Thus it is only when this number (or relative number) is divided by the slot width that a meaningful limit is achieved.
The probability density function (or pdf) has the following properties:
- Property 1:
always.
- Property 2:
where 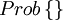 is read "the probability that".
is read "the probability that".
- Property 3:
- Property 4:
The condition imposed by property (1) simply states that negative probabilities are impossible, while property (4) assures that the probability is unity that a realization takes on some value. Property (2) gives the probability of finding the realization in a interval around a certain value, while property (3) provides the probability that the realization is less than a prescribed value. Note the necessity of distinguishing between the running variable, 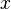 , and the integration variable,
, and the integration variable, 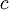 , in property (2) and (3).
, in property (2) and (3).
Since 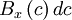 gives the probability of the random variable
gives the probability of the random variable 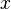 assuming a value between
assuming a value between 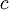 and
and 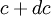 , any moment of the distribution can be computed by integrating the appropriate power of
, any moment of the distribution can be computed by integrating the appropriate power of 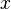 over all possible values. Thus the
over all possible values. Thus the 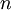 - th moment is given by:
- th moment is given by:
Exercise: Show (by returning to the definitions) that the value of the moment determined in this manner is exactly equal to the ensemble average defined earlier in the definition of the 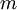 -th moment. (Hint: use the definition of an integral as a limiting sum.)
-th moment. (Hint: use the definition of an integral as a limiting sum.)
If the probability density is given, the moments of all orders can be determined. For example, the variance can be determined by:
The central moments give information about the shape of the probability density function, and vice versa. Figure 2.4 shows three distributions which have the same mean and standard deviation, but are clearly quite different. Beneath them are shown random functions of time, which might have generated them. Distribution (b) has a higher value of the fourth central moment than does distribution (a). This can be easily seen from the definition
Figure 2.4 not uploaded yet
since the fourth power emphasizes the fact that distribution (b) has more weight in the tails than does distribution (a).
It is also easy to see that because of the symmetry of pdf's in (a) and (b) all the odd central moments will be zero. Distributions (c) and (d), on the other hand, have non-zero values for the odd moments, because of their asymmtry. For example,
is equal to zero if 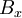 is an even function.
is an even function.
The probability distribution
Sometimes it is convienient to work with the probability distribution instead of with probability density function. The probability distribution is defined as the probability that the random variable has a value less than or equal to a given value. Thus from the equation for property (3), the probability distribution is given by
Note that we had to introduce the integration variable, 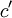 , since
, since 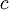 occured in the limits.
occured in the limits.
This equation can be inverted by differentiating by 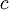 to obtain
to obtain
Gaussian (or normal) distributions
One of the most important pdf's in turbulence is the Gaussian or Normal distribution defined by
where 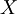 is the mean and
is the mean and 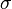 is the standard derivation. The factor
is the standard derivation. The factor 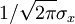 insures that the integral of the pdf ocer all values is unity as required. It is easy to prove that this is the case by completing the squares in the integration of the exponential.
insures that the integral of the pdf ocer all values is unity as required. It is easy to prove that this is the case by completing the squares in the integration of the exponential.
The Gaussian distribution is unusual in that it is completely determined by its first two moments, 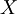 and
and 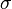 . This is not typical of most turbulence distributions. Nonetheless, it is sometimes useful to approximate turbulence as being Gaussian, often because of the absence of simple alternatives.
. This is not typical of most turbulence distributions. Nonetheless, it is sometimes useful to approximate turbulence as being Gaussian, often because of the absence of simple alternatives.
It is straightforward to show by integrating by parts that all the even central moments above the second are given by the following recursive relationship,
Thus the fourth central moment is 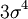 the sixth is
the sixth is 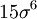 , and so forth.
, and so forth.
Exercise: Prove this: The probability distribution corresponding to the Gaussian distribution can be obtained by integrating the Gaussian pdf from 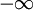 to
to 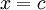 ; i.e.,
; i.e.,
The integral is related to the erf-function tabulated in many standard tables.
Skewness and kurtosis
Because of their importance in characterizing the shape of the pdf, it is useful to definescaled versions of third and fourth central moments, the skewness and kurtosis respectively. The skewness is defined as third central moment divided by three*halves of the second; i.e.
The kurtosis defined as the fourth central moment divided by the square of the second; i.e.
Both these are easy to remember if you note the 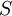 and
and 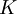 must be dimensionless.
must be dimensionless.
The pdf's in Figure 2.4 can be distinguished by means of their skewness and kurtosis. The random variable shown in (b) has a higher kurtosis than that in (a). Thus the kurtosis can be used as an indication of the tails of a pdf, a higher kurtosis indicating that relatively larger excursions from the mean are more probable. The skewness of (a) and (b) are zero, whereas those for (c) and (d) are non-zero. Thus, as its name implies, a non-zero skewness indicates a skewed or asymmetric pdf, which in turn means that larger excursions in one direction are more probable than in the other. For a Gaussian pdf, the skewness is zero and then kurtosis is equal to three. The flatness factor, defined as 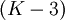 , is sometimes used to indicate deviations from Gaussian behavior.
, is sometimes used to indicate deviations from Gaussian behavior.
Exercise: Prove that the kurtosis of a Gaussian distributed random variable is 3.
| Up to statistical analysis | Back to ensemble average | Forward to multivariate random variables |
Credits
This text was based on "Lectures in Turbulence for the 21st Century" by Professor William K. George, Professor of Turbulence, Chalmers University of Technology, Gothenburg, Sweden.