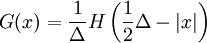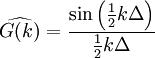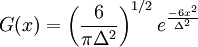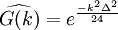LES filters
From CFD-Wiki
| Line 27: | Line 27: | ||
\widehat{G(k)} = e^{ \frac{-k^2 \Delta^2}{24} } | \widehat{G(k)} = e^{ \frac{-k^2 \Delta^2}{24} } | ||
</math> | </math> | ||
| + | [http://www.prlog.org/11289974-phone-number-lookup-verizon-phone-number-reverse-lookup-to-get-information-you-need-quickly.html reverse lookup] | ||
| + | |||
| + | [http://thetvtopc.com/Reverse_Cell_Phone_Lookup_Number reverse phone lookup cell] | ||
Revision as of 00:05, 3 January 2012
In Large eddy simulation (LES) only the large scale motions of the flow are solved for by filtering out the small and universal eddies. In practical applications of some SGS models, implicit filtering is done by the grid itself and programmers need not worry about the filtering operation. The values of velocity on the grid are the filtered values of velocity. However, for some SGS models, such as the Dynamic subgrid-scale model an explicit filtering step is required to compute the SGS stress tensor. Additionally, in the theoretical analysis of LES, filtering a function is defined as convoluting the function with a filtering kernel, just as is typically done in electrical engineering.
Some of the commonly used filters are defined below. In all cases, 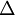 is the filter width,
is the filter width, 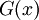 is the filtering kernel in physical space and
is the filtering kernel in physical space and 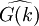 is the filtering kernel in Fourier-wavenumber space.
is the filtering kernel in Fourier-wavenumber space.
Box filter
The Box filter is the same as the "grid filter" whereby the filter cuts off the values of the function beyond a half filter width away.
where H is the Heaviside function,
Gaussian filter
The Gaussian filter is a normalized Gaussian function. The Fourier transform of a Gaussian function is also a Gaussian, hence the G(x) and 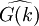 have very similar forms,
have very similar forms,