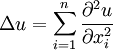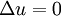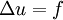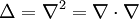Laplacian
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
The n-dimensional Laplacian operator in Cartesian coordinates is defined by | The n-dimensional Laplacian operator in Cartesian coordinates is defined by | ||
| - | <math> | + | :<math> |
\Delta u = \sum_{i=1}^n \frac{\partial^2 u}{\partial x_i^2} | \Delta u = \sum_{i=1}^n \frac{\partial^2 u}{\partial x_i^2} | ||
</math> | </math> | ||
| Line 9: | Line 9: | ||
* Laplace equation | * Laplace equation | ||
| - | <math> | + | :<math> |
\Delta u = 0 | \Delta u = 0 | ||
</math> | </math> | ||
| Line 15: | Line 15: | ||
* Poisson equation | * Poisson equation | ||
| - | <math> | + | :<math> |
\Delta u = f | \Delta u = f | ||
</math> | </math> | ||
| Line 22: | Line 22: | ||
The Laplacian operator is invariant under coordinate rotation. | The Laplacian operator is invariant under coordinate rotation. | ||
| + | |||
| + | The Laplace operator is also denoted as <math>\nabla^2</math> since it is the divergence of the gradient operator | ||
| + | |||
| + | :<math> | ||
| + | \Delta = \nabla^2 = \nabla \cdot \nabla | ||
| + | </math> | ||
| + | |||
| + | == Laplacian in cylindrical coordinates == | ||
| + | |||
| + | If <math>(x,r,\phi)</math> are cylindrical coordinates, then the Laplacian of a scalar field variable <math>u</math> is | ||
| + | |||
| + | :<math> | ||
| + | \Delta u = \frac{\partial^2 u}{\partial x^2} + \frac{1}{r} \frac{\partial}{\partial r} \left( r \frac{\partial u}{\partial r} \right) + \frac{1}{r^2} \frac{\partial^2 u}{\partial \phi^2} | ||
| + | </math> | ||
| + | |||
| + | == Laplacian in spherical coordinates == | ||
| + | |||
| + | If <math>(r,\theta,\phi)</math> are spherical coordinates, then the Laplacian of a scalar field variable <math>u</math> is | ||
| + | |||
| + | :<math> | ||
| + | \Delta u = | ||
| + | \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial u}{\partial r} \right) + | ||
| + | \frac{1}{r^2 \sin\theta} \frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial u}{\partial \theta} \right) + | ||
| + | \frac{1}{r^2 \sin^2\theta} \frac{\partial^2 u}{\partial \phi^2} | ||
| + | </math> | ||
Revision as of 06:27, 13 September 2005
The n-dimensional Laplacian operator in Cartesian coordinates is defined by
It is an important differential operator which occurs in many equations of mathematical physics and is usually associated with dissipative effects. Some of the important equations are
- Laplace equation
- Poisson equation
Solutions of these equations are very smooth and in most cases are infinitely differentiable (when the associated data of the problem are sufficiently smooth).
The Laplacian operator is invariant under coordinate rotation.
The Laplace operator is also denoted as  since it is the divergence of the gradient operator
since it is the divergence of the gradient operator
Laplacian in cylindrical coordinates
If  are cylindrical coordinates, then the Laplacian of a scalar field variable
are cylindrical coordinates, then the Laplacian of a scalar field variable 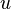 is
is
Laplacian in spherical coordinates
If 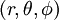 are spherical coordinates, then the Laplacian of a scalar field variable
are spherical coordinates, then the Laplacian of a scalar field variable 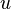 is
is