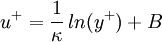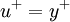Law of the wall
From CFD-Wiki
(Difference between revisions)
(changing "B" constant in formula to "C" constant so that the formula gets consistent with the "Where :" list of parameters) |
m (Changed constant in formula and table from C to B to match formula in plot) |
||
| Line 1: | Line 1: | ||
In the log layer the velocity profile can be estimated with the log law: | In the log layer the velocity profile can be estimated with the log law: | ||
| - | :<math>u^+ = \frac{1}{\kappa} \, ln(y^+) + | + | :<math>u^+ = \frac{1}{\kappa} \, ln(y^+) + B</math> |
and close to the wall in the viscous sublayer | and close to the wall in the viscous sublayer | ||
| Line 17: | Line 17: | ||
|<math>\kappa</math> || von Karman's constant (<math>\approx 0.41</math>) | |<math>\kappa</math> || von Karman's constant (<math>\approx 0.41</math>) | ||
|- | |- | ||
| - | |<math> | + | |<math>B</math> || Constant (<math>\approx 5.1</math>) |
|} | |} | ||
Revision as of 20:15, 5 September 2011
In the log layer the velocity profile can be estimated with the log law:
and close to the wall in the viscous sublayer
Where:
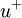
Dimensionless velocity 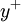
Dimensionless wall distance 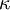
von Karman's constant ( 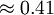 )
)
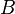
Constant ( 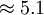 )
)
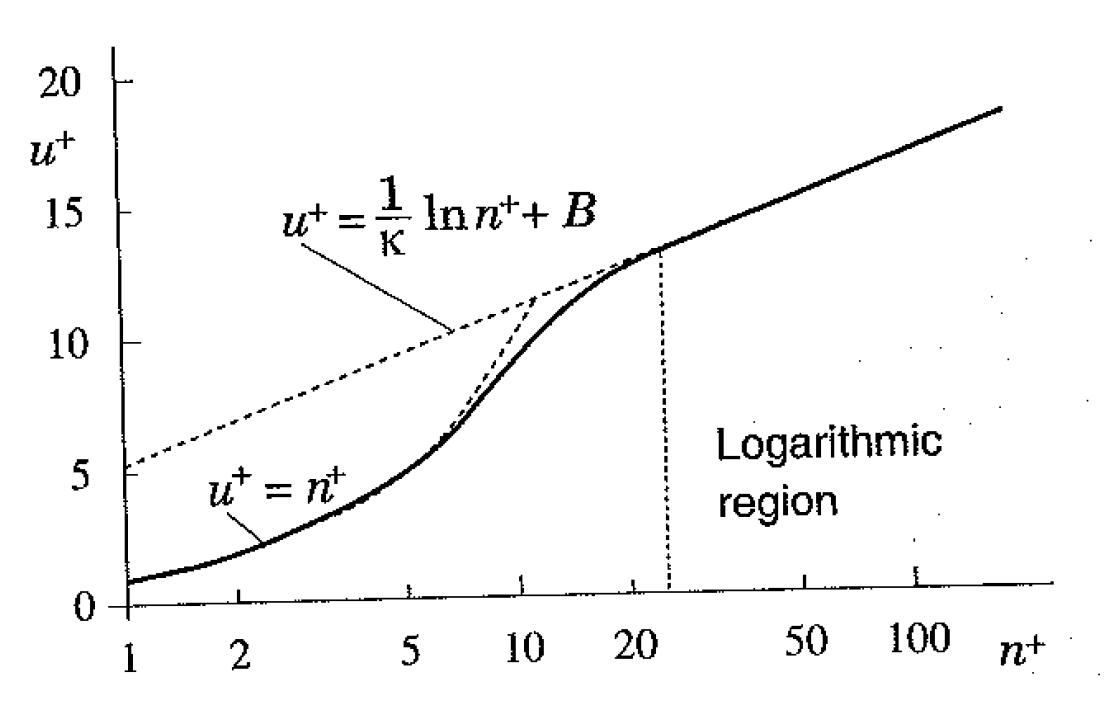
We should have a lin-log plot here of a typical turbulent boundary layer to illustrate where the log-law is valid, anyone have one handy?
In the image y is replaced with the letter n.