Machine precision
From CFD-Wiki
| Line 58: | Line 58: | ||
| - | Machine precision must be taken into consideration while writing numerical programs. The choice between single and double precision must be made judiciously. For example, while performing turbulent Navier-Stokes computations, the grid is highly clustered near solid walls. The difference between neighbouring grid points can be very small which requires using double precision. The choice of equations can also be important and can be made intelligently. For example, if you want to compute 1 - cos(x) for a very small value of x then it is better to use the identical expression 2 | + | Machine precision must be taken into consideration while writing numerical programs. The choice between single and double precision must be made judiciously. For example, while performing turbulent Navier-Stokes computations, the grid is highly clustered near solid walls. The difference between neighbouring grid points can be very small which requires using double precision. The choice of equations can also be important and can be made intelligently. For example, if you want to compute <math>1 - \cos(x)</math> for a very small value of x then it is better to use the identical expression <math>2 \sin^2(x/2)</math> since the former expression is susceptible to round-off error due to machine precision. |
Latest revision as of 04:14, 29 November 2005
Machine precision is the smallest number ε such that the difference between 1 and 1 + ε is nonzero, ie., it is the smallest difference between two numbers that the computer recognizes. On a 32 bit computer, single precision is 2-23 (approximately 10-7) while double precision is 2-52 (approximately 10-16) . The following fortran program finds the machine precision (This is based on a mailing list posting by Guido Pagnacco).
PROGRAM MAIN
IMPLICIT NONE
DOUBLE PRECISION DEPS, DA
REAL EPS, A
INTEGER N, DN
EPS = 1.0
DEPS = 1.0D0
N = 0
DN = 0
C determination of epsilon for reals (single precision)
1 EPS = EPS / 2.0
A = EPS + 1.0
C PRINT *, A
IF (A .GT. 1.0) THEN
N = N + 1
GO TO 1
ELSE
EPS = ABS(2.0 * EPS)
END IF
C determination of epsilon for double precision
2 DEPS = DEPS / 2.0D0
DA = DEPS + 1.0D0
C PRINT *, DA
IF (DA .GT. 1.0D0) THEN
DN = DN + 1
GO TO 2
ELSE
DEPS = DABS(2.0D0 * DEPS)
END IF
IF(N .eq. DN)THEN
PRINT*,'Your computer probably has a math coprocessor.'
PRINT*,'Uncomment the two print statements and rerun.'
STOP
ENDIF
WRITE(*,9) -N
9 FORMAT(40x,i3)
WRITE(*,10) eps
10 FORMAT(' Single precision =',e16.8,' or 2')
WRITE(*,9) -DN
WRITE(*,12) deps
12 FORMAT(' Double precision =',e16.8,' or 2')
STOP
END
The above program finds the largest number N such that the difference between 1 and 1 + 2-N is nonzero which gives the machine precision. Computers also have a secondary processor for floating point operations (sometimes called Floating Point Unit or FPU). A note of caution about this routine: many compilers will optimize it to run completely inside the math coprocessor of your computer (if it has one). But coprocessors usually perform their internal computations in what is sometimes called long double precision format (the number is 80 bit instead of 64 for the double and 32 for the real). This results in the routine giving out the same value for both the epsilon in real and double precisions, usually a value of 2-64 if the machine works by IEEE standards. To avoid that it is necessary to force the routine to exit from the coprocessor every cycle. A dirt solution is the one implemented above: print something.
Machine precision must be taken into consideration while writing numerical programs. The choice between single and double precision must be made judiciously. For example, while performing turbulent Navier-Stokes computations, the grid is highly clustered near solid walls. The difference between neighbouring grid points can be very small which requires using double precision. The choice of equations can also be important and can be made intelligently. For example, if you want to compute 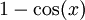 for a very small value of x then it is better to use the identical expression
for a very small value of x then it is better to use the identical expression 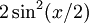 since the former expression is susceptible to round-off error due to machine precision.
since the former expression is susceptible to round-off error due to machine precision.
