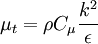Realisable k-epsilon model
From CFD-Wiki
(Difference between revisions)
(c_2 = 1.92) |
|||
| Line 31: | Line 31: | ||
==Model Constants == | ==Model Constants == | ||
| - | <math> C_{1 \epsilon} = 1.44, \;\; C_2 = 1. | + | <math> C_{1 \epsilon} = 1.44, \;\; C_2 = 1.92, \;\; \sigma_k = 1.0, \;\; \sigma_{\epsilon} = 1.2 </math> |
[[Category:Turbulence models]] | [[Category:Turbulence models]] | ||
Revision as of 15:09, 22 August 2013
Transport Equations
Where
![C_1 = \max\left[0.43, \frac{\eta}{\eta + 5}\right] , \;\;\;\;\; \eta = S \frac{k}{\epsilon}, \;\;\;\;\; S =\sqrt{2 S_{ij} S_{ij}}](/W/images/math/1/9/3/193f62d995a6b0190d41325b612bf336.png)
In these equations, 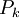 represents the generation of turbulence kinetic energy due to the mean velocity gradients, calculated in same manner as standard k-epsilon model.
represents the generation of turbulence kinetic energy due to the mean velocity gradients, calculated in same manner as standard k-epsilon model. 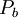 is the generation of turbulence kinetic energy due to buoyancy, calculated in same way as standard k-epsilon model.
is the generation of turbulence kinetic energy due to buoyancy, calculated in same way as standard k-epsilon model.
Modelling Turbulent Viscosity
where
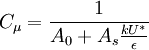
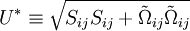 ;
;
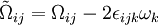 ;
;
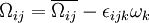
where 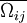 is the mean rate-of-rotation tensor viewed in a rotating reference frame with the angular velocity
is the mean rate-of-rotation tensor viewed in a rotating reference frame with the angular velocity 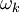 . The model constants
. The model constants 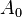 and
and 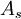 are given by:
are given by:
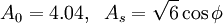
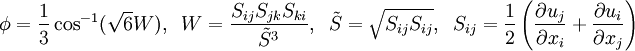
Model Constants
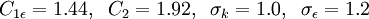

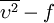 model
model
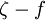 model
model
![\frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_j} (\rho k u_j) = \frac{\partial}{\partial x_j} \left [ \left(\mu + \frac{\mu_t}{\sigma_k}\right) \frac{\partial k} {\partial x_j} \right ] + P_k + P_b - \rho \epsilon - Y_M + S_k](/W/images/math/0/0/4/004f9597d5f640c6152d7ee7ec2af16a.png)
![\frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_j} (\rho \epsilon u_j) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_{\epsilon}}\right) \frac{\partial \epsilon}{\partial x_j} \right ] + \rho \, C_1 S \epsilon - \rho \, C_2 \frac{{\epsilon}^2} {k + \sqrt{\nu \epsilon}} + C_{1 \epsilon}\frac{\epsilon}{k} C_{3 \epsilon} P_b + S_{\epsilon}](/W/images/math/9/e/1/9e195cf17f086a6a1ad3914571b491ba.png)