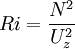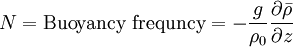Richardson number
From CFD-Wiki
(Difference between revisions)
Discoganya (Talk | contribs) |
|||
| Line 11: | Line 11: | ||
Here <math> \rho_0 </math> is the reference density and <math> \bar{\rho} </math> is the background density field. | Here <math> \rho_0 </math> is the reference density and <math> \bar{\rho} </math> is the background density field. | ||
| + | |||
| + | ==References== | ||
| + | |||
| + | *{{reference-book |author=Hunt, J C R | year=1998 | title= Lewis Fry Richardson and his contributions to mathematics, meteorology, and models of conflict| rest =Annual Review of Fluid Mechanics, Vol. 30, 1998, pp. xiii–xxxvi}} | ||
Latest revision as of 15:37, 16 January 2008
In the stability of continuously stratified parallel shear flows the ratio of (the squares of) the buoyancy frequency to the background velocity gradient is known as the (gradient) Richardson number.
Here 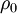 is the reference density and
is the reference density and 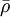 is the background density field.
is the background density field.
References
- Hunt, J C R (1998), Lewis Fry Richardson and his contributions to mathematics, meteorology, and models of conflict, Annual Review of Fluid Mechanics, Vol. 30, 1998, pp. xiii–xxxvi.