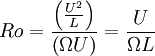Rossby number
From CFD-Wiki
(Difference between revisions)
Discoganya (Talk | contribs) |
Discoganya (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | [[Category:Dimensionless parameters]] | ||
| + | |||
In [[rotating flows]] (e.g. [[geophysical flows]]), the Rossby number is defined as the ratio of the advective acceleration to the [[Corioilis force|Coriolis acceleration]]. Alternately, it may be thought of as the ratio of the [[inertial force]] to the [[Coriolis force]]. | In [[rotating flows]] (e.g. [[geophysical flows]]), the Rossby number is defined as the ratio of the advective acceleration to the [[Corioilis force|Coriolis acceleration]]. Alternately, it may be thought of as the ratio of the [[inertial force]] to the [[Coriolis force]]. | ||
Latest revision as of 20:29, 22 September 2005
In rotating flows (e.g. geophysical flows), the Rossby number is defined as the ratio of the advective acceleration to the Coriolis acceleration. Alternately, it may be thought of as the ratio of the inertial force to the Coriolis force.
where 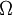 is the angular speed of rotation, U is the velocity scale and L is the lenth scale.
is the angular speed of rotation, U is the velocity scale and L is the lenth scale.