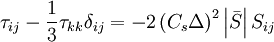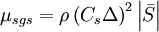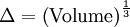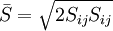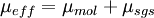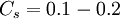Smagorinsky-Lilly model
From CFD-Wiki
(Difference between revisions)
m |
m |
||
| Line 1: | Line 1: | ||
The Smagorinsky model could be summerised as: | The Smagorinsky model could be summerised as: | ||
:<math> | :<math> | ||
| - | \tau _{ij} - \frac{1}{3}\tau _{kk} \delta _{ij} = - 2\left( {C_s | + | \tau _{ij} - \frac{1}{3}\tau _{kk} \delta _{ij} = - 2\left( {C_s \Delta } \right)^2 \left| {\bar S} \right|S_{ij} |
</math> <br> | </math> <br> | ||
| Line 8: | Line 8: | ||
:<math> | :<math> | ||
| - | \mu _{sgs} = \rho \left( {C_s | + | \mu _{sgs} = \rho \left( {C_s \Delta } \right)^2 \left| {\bar S} \right| |
</math> | </math> | ||
<br> | <br> | ||
| Line 14: | Line 14: | ||
Where the filter width is usually taken to be | Where the filter width is usually taken to be | ||
:<math> | :<math> | ||
| - | + | \Delta = \left( \mbox{Volume} \right)^{\frac{1}{3}} | |
</math> | </math> | ||
<br> | <br> | ||
Revision as of 12:20, 8 May 2006
The Smagorinsky model could be summerised as:
In the Smagorinsky-Lilly model, the eddy viscosity is modeled by
Where the filter width is usually taken to be
and
The effective viscosity is calculated from
The Smagorinsky constant usually has the value: