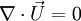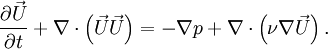Solution of Navier-Stokes equations
From CFD-Wiki
| (8 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | ==Introduction== | |
| - | + | Most traditional CFD algorithms require the solution of the Navier-Stokes (N-S) equations. There are two important issues that arise in the solution process: | |
| - | + | # The N-S equations are nonlinear. | |
| - | + | # The pressure-velocity coupling often requires special consideration. | |
| - | + | The details of the solution process depend upon the details of the flow to be solved. The solution process for a incompressible flow can be very different than that for a compressible flow. | |
| - | + | ||
| - | + | ||
| + | ==Incompressible flow== | ||
| + | In situations in which the density is approximately constant, the flow may be termed [[Incompressible flow |incompressible]]. The Navier-Stokes equation may then be written as a continuity equation | ||
| - | + | :<math> | |
| - | + | \nabla \cdot \vec U = 0 </math> | |
| - | + | ||
| - | = | + | |
| - | + | ||
| - | + | and as a momentum equation | |
| - | + | :<math> {{\partial \vec U} \over {\partial t}} + \nabla \cdot \left( {\vec U\vec U} \right) = - \nabla p + \nabla \cdot\left( {\nu \nabla \vec U} \right). </math> | |
| - | + | ||
| - | + | ||
| - | + | ||
| + | Here, we have written the nonlinear convective term (the second term on the right-hand side) in the so-called conservative form. If a turbulence model is to be employed, then the equations will change. If an eddy viscosity approach is to be used, then there are three likely modifications: | ||
| + | *the flow variables will represent average (or filtered) quantities, | ||
| + | *the viscosity <math>\nu</math> will actually be the sum of the fluid property and the calculated eddy viscosity (and will then be nonconstant, justifying keeping it inside the divergence operator), and | ||
| + | *the pressure will be modified to include normal-stress-like terms arising from the eddy viscosity assumption. | ||
| - | + | Thus, the equation as written will be valid for both turbulent or laminar flows, with some modification of the actual meaning of individual terms. | |
| + | It is somewhat difficult to categorize the solution methods for the incompressible N-S equations, as over the years many have been developed that are very similar. However, the manner in which the difficulties associated with the pressure solution are handled (a process made difficult by the fact that pressure does not appear in the continuity equation) can be used to broadly categorize methods. | ||
| - | + | ==Compressible Flow== | |
| - | + | ||
Latest revision as of 10:01, 23 April 2009
Introduction
Most traditional CFD algorithms require the solution of the Navier-Stokes (N-S) equations. There are two important issues that arise in the solution process:
- The N-S equations are nonlinear.
- The pressure-velocity coupling often requires special consideration.
The details of the solution process depend upon the details of the flow to be solved. The solution process for a incompressible flow can be very different than that for a compressible flow.
Incompressible flow
In situations in which the density is approximately constant, the flow may be termed incompressible. The Navier-Stokes equation may then be written as a continuity equation
and as a momentum equation
Here, we have written the nonlinear convective term (the second term on the right-hand side) in the so-called conservative form. If a turbulence model is to be employed, then the equations will change. If an eddy viscosity approach is to be used, then there are three likely modifications:
- the flow variables will represent average (or filtered) quantities,
- the viscosity
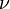 will actually be the sum of the fluid property and the calculated eddy viscosity (and will then be nonconstant, justifying keeping it inside the divergence operator), and
will actually be the sum of the fluid property and the calculated eddy viscosity (and will then be nonconstant, justifying keeping it inside the divergence operator), and
- the pressure will be modified to include normal-stress-like terms arising from the eddy viscosity assumption.
Thus, the equation as written will be valid for both turbulent or laminar flows, with some modification of the actual meaning of individual terms.
It is somewhat difficult to categorize the solution methods for the incompressible N-S equations, as over the years many have been developed that are very similar. However, the manner in which the difficulties associated with the pressure solution are handled (a process made difficult by the fact that pressure does not appear in the continuity equation) can be used to broadly categorize methods.