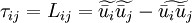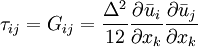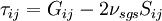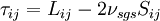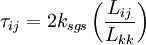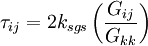Structural modeling
From CFD-Wiki
(Difference between revisions)
| Line 22: | Line 22: | ||
</math> | </math> | ||
| - | Dynamic structure models | + | Dynamic structure models (non-viscosity version) |
:<math> | :<math> | ||
| - | \tau_{ij} = 2k_{sgs} \frac{L_{ij}}{L_{kk}} | + | \tau_{ij} = 2k_{sgs} \left(\frac{L_{ij}}{L_{kk}}\right) |
</math> | </math> | ||
or | or | ||
:<math> | :<math> | ||
| - | \tau_{ij} = 2k_{sgs} \frac{G_{ij}}{G_{kk}} | + | \tau_{ij} = 2k_{sgs} \left(\frac{G_{ij}}{G_{kk}}\right) |
</math> | </math> | ||
Revision as of 22:09, 24 June 2013
Those that use the physical hypothesis of scale similarity
Those derived by formal series expansions
Mixed models, which are based on linear combinations of the eddy-viscosity and structural types
or
Dynamic structure models (non-viscosity version)
or